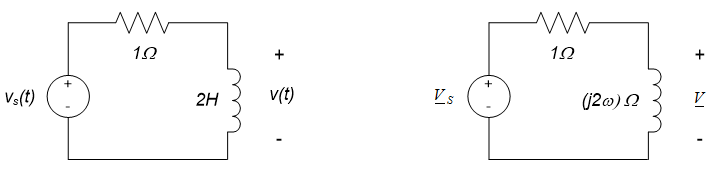In section 10.6, we saw that a system’s frequency response provided a steady-state input-output relationship for a system, as a function of frequency. We could apply this frequency response to the phasor representation of the input signal in order to determine the system’s steady-state sinusoidal response – we simply evaluated the frequency response at the appropriate frequencies to determine the effect of the system on the input sinusoids. This approach had the potential for simplifying our analysis considerably, particularly for the case in which the input signal contained multiple sinusoids with different frequencies.

In Chapter 10, the signals we considered consisted only of individual sinusoids. It is more useful, however, in some ways to think in terms of the inputs and outputs of the system as functions of frequency, in the same way in which we considered the frequency response of the system to be a function of frequency in section 10.6. We can then perform our analysis of the system entirely in terms of the frequencies involved. This leads to the use of the system’s frequency response directly as a design and analysis tool. In many cases, this means that the actual time- domain behavior of the system or signal is of limited interest (or in some cases, not considered at all). Some examples of frequency domain analyses are:

1. Determining dominant sinusoidal frequency components in a measured signal. Complex signals can often be represented as a superposition of several sinusoidal components with different frequencies. Identifying sinusoidal components with large amplitudes (the so-called dominant frequencies) can help with many design problems. One application of this is in the area of combustion instability – combustion processes in rocket engines can become unstable due to a variety of reasons, any of which can result in catastrophic failure of the engine. The type of instability which occurs is generally linked to a particular frequency; identification of the frequency of the pressure oscillations associated with the combustion instability is generally the first step in determining the cause of the instability.
2. Designing systems to provide a desired frequency response. Audio components in stereo systems are generally designed to produce a desired frequency response. A graphic equalizer, for example, can be used to boost (or amplify) some frequency ranges and attenuate other frequency ranges. When adjusting the settings on an equalizer, you are essentially directly adjusting the system’s frequency response to provide a desired system response.

This chapter begins in section 11.1 with a brief review of frequency responses and an overview of the use of the frequency response in system analysis and design. In section 11.2, we discuss representation of signals in terms of their frequency content. At this time, we will also represent the frequency content of the input and output signals and the frequency response of the system in graphical format – this helps us visualize the frequency content of the signals and system. This leads us to think in terms of using a system to create a signal with a desired frequency content – this process is called filtering and is discussed in section 11.3. Using logarithmic scales to represent the signal and system frequency responses can – in many cases – simplify the analysis or design process; this format of presentation is called a Bode plot, and they are very briefly introduced in section 11.4. We will discuss Bode plots in more depth in later chapters.

It is important to keep in mind that, when we are performing frequency domain analyses, we are restricting our attention to the steady-state sinusoidal response of the system. Frequency domain design and analysis methods are so pervasive that they are often used to infer the system’s transient response and/or its response to non- sinusoidal signals, so it is sometimes possible to forget the origins and limitations of the original concepts!

• Use the frequency response of a system to determine the frequency domain response of a system to a given input
• State from memory the definition of signal spectrum
• Create plots of given signal spectra
• Plot a circuit’s magnitude and phase responses
• Check a circuit’s amplitude response at low and high frequencies against the expected physical behavior of the circuit
• Graphically represent a system’s frequency domain response from provided signal spectra plots and plots of the system’s frequency response
• Identify low pass and high pass filters
• Calculate a system’s cutoff frequency
• Determine the DC gain of an electrical circuit
• Write, from memory, the equation used to convert gains to decibel form
• Sketch straight-line amplitude approximations to Bode plots
• Sketch straight-line phase approximations to Bode plots

In section 10.6, we defined the frequency response $H(j \omega)$ of a system as a complex function of frequency which describes the relationship between the steady state sinusoidal response of a system and the corresponding sinusoidal input. Thus, if a sinusoidal input with some frequency $\omega_0$ is applied to a system with frequency response $H(j \omega)$, the amplitude of the output sinusoid is the input sinusoid’s amplitude multiplied by the magnitude response of the system, evaluated at the frequency $\omega_0$. The phase angle of the output sinusoid is the sum of the input sinusoid’s phase and the phase response of the system, evaluated at the frequency $\omega_0$. The overall idea is presented in block diagram form in Figure 11.1 below.

The true power of the frequency response is, however, if we consider both the system’s input and output phasors to be complex functions of frequency, in the same way that the frequency response is a complex function of frequency. In this case, the block diagram of Figure 11.1 can be represented as shown in Figure 11.2.

In Figure 11.2, the output is determined by multiplying the phasor representation of the input by the system’s frequency response. It is important to keep in mind that the arguments of this multiplication are complex functions of frequency – both the input and the frequency response at any frequency are complex numbers, so the output at any frequency is also a complex number. We typically use polar form to represent these complex numbers, so the amplitude of the output signal is the product of the amplitude of the input signal and the magnitude response of the system and the phase of the output signal is the sum of the phase of the input and the phase response of the system. Mathematically, these are expressed as:

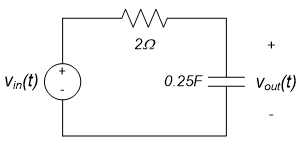
$$|\underline{Y}(j \omega)|=|\underline{U}(j \omega)| \cdot |H (j \omega)| (Eq. 11.1) And $$\angle \underline{Y}(j \omega) = \angle \underline{U}(j \omega) + \angle H(j \omega) (Eq. 11.2)$$ We now present two examples of the process defined by equations (11.1) and (11.2) above. ---- ==== Example 11.1 ==== Determine the phasor representation for $v_{out}(t)$ in the circuit shown below as a function of frequency, if the input voltage is $v_{in}(t) = 3 \cos(2t+20^{\circ}) + 7 \cos(4t-60^{\circ})$. (Note: this problem is the same as that of Example 10.19 of chapter 10.6; the difference is primarily philosophical.)

The frequency response of this circuit, for arbitrary resistance and capacitance values, was determined in example 10.18 of chapter 10.6. For our specific resistor and capacitor values, this becomes:

$$H(j \omega) = \frac{1}{1+j \omega RC} = \frac{1}{1+j \omega(2 \Omega)(0.25F)} = \frac{1}{1+j \omega(0.5)} = \frac{2}{2+j \omega}$$

We can represent the input as a piecewise function of frequency:

$$\underline{V}_{in} = \begin{cases} 3 \angle 20^{\circ}, & \omega = 2 \text{rad/sec} \\ 7 \angle -60^{\circ}, & \omega = 4 \text{rad/sec} \\ 0, & \text{otherwise} \end{cases} $$

The input phasor is now considered to be a function of frequency, whose only nonzero components are at frequencies of 2 rad/sec and 4 rad/sec.

The phasor output is simply the product of the input phasor as a function of frequency and the frequency response. For frequencies other than 2 rad/sec and 4 rad/sec, the input is zero and the frequency response is finite, so the output is zero. We determined the output phasor at frequencies of 2 and 4 rad/sec in example 10.19 in section 10.6; using those results allows us to write the output phasor directly as:

$$\underline{V}_{out} = \begin{cases} \frac{3}{\sqrt{2}} \angle -25^{\circ}, & \omega = 2 \text{rad/sec} \\ \frac{7}{\sqrt{5}} \angle -123.4^{\circ}, & \omega = 4 \text{rad/sec} \\ 0, & \text{otherwise} \end{cases} $$

The frequency response of a system, $H(j \omega)$, and the frequency domain input to the system, $\underline{U}(j \omega)$, are given below. The frequency response is dimensionless, the input has units of volts, and the units of frequency are rad/sec. Determine the system output $\underline{Y}(j \omega)$.

$$\underline{U}_{j \omega} = \begin{cases} j \omega, & 0 < \leq 1 \\ j(2-\omega), & 1< \omega < 2 \\ 0, & \text{otherwise} \end{cases} $$

$$\underline{U}_{j \omega} = \begin{cases} 0, & 0 < \omega \leq 0.5 \\ 1, & 0.5 < \omega \leq 1.5 \\ 0, & \text{otherwise} \end{cases} $$

The system output is determined from a point-by-point multiplication of the input and the frequency response. In this case, both the input to the system and the system frequency response are defined as piecewise functions of frequency, so we must perform a piecewise multiplication to obtain the output. The output, for various ranges of frequency, is obtained below:

$0 < \omega \leq 0.5$:

• In this range, $H(j \omega) =0$ and the input is finite, so $\underline{Y}(j \omega)=0$.

$0.5 < \omega \leq 1.5$:

• In this range, $H(j \omega)=1$ and $\underline{U}(j \omega)= j \omega$, so the output is: $\underline{Y}=(1)(j \omega)=j \omega$

$1< \omega \leq 1.5$:

• In this range, $H(j \omega)=1$ and $\underline{U}(j \omega)=j(2-\omega)$, so the output is: $\underline{Y}=j(2-\omega)$.

$1.5< \omega \leq 2$:

• In this range, $H(j \omega)=0$ and the input is finite, so $\underline{Y}(j \omega)=0$.

For any other value of frequency, both the input and the frequency response are zero, so the output is obviously zero.

The above results allow us to define the system output in a piecewise fashion as:

$$\underline{Y}_{j \omega} = \begin{cases} {j \omega}, & 0.5 < \omega \leq 1 \\ j(2- \omega), & 1 < \omega \leq 1.5 \\ 0, & \text{otherwise} \end{cases} $$

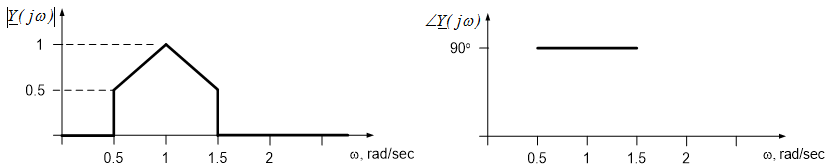
For the signals of example 11.2, plot: the magnitude and phase responses of the system and the magnitude and phase of both the input and output signals. The magnitude and phase response of the system are shown to the left and right below. The phase of the input is indicated as zero for all frequencies, since the input is real-valued for all frequencies. Strictly speaking, however, the phase is not well defined when the magnitude response is zero. (The phase angle provides the direction of a number from the origin of the complex plane, it is difficult to tell what direction “zero” is from itself!)

The magnitude and phase of the frequency domain input are shown below. The $90^{\circ}$ phase shift over the range of 0 to 2 rad/sec is due to the factor of “j” in the frequency response. The phase is not indicated where the input amplitude is zero; this is again because the phase angle of “zero” is not well defined.

The magnitude and phase of the output are shown below. It is easy to see from the above figures that the magnitude of the output is the product of the input magnitude and the magnitude response and the phase of the output is the sum of the input phase and the phase response.

The above system is performing a potentially useful operation. Any sinusoidal signals with frequencies between 0.5 and 1.5 rad/sec are passed through the system (they appear at the output, unchanged). Sinusoids with frequencies outside this range are eliminated by the system – they are not present in the system’s output. This system is performing what is called a band-pass operation; frequencies within a certain frequency band are passed through the system, while all other frequencies are stopped. This type of operation can be useful, for example, in communication systems – signals from different radio stations should not overlap or they will interfere with one another.

A very powerful analysis and design techniques for linear systems consists of considering the input and output signals to be phasors which are functions of frequency, so that the amplitude and phase of the input and output signals are both defined at each value of frequency. If this viewpoint is taken,

• The amplitude of the output signal is the frequency-by-frequency product of the amplitude of the input signal and the magnitude response of the system, and
• The phase of the output signal is the frequency-by-frequency sum of the phase of the input and the phase

response of the system.

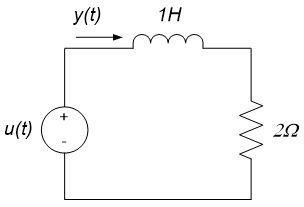
1. Calculate the frequency response for the circuit below, if $u(t)$ is the input and $y(t)$ is the output.

2. The input to a system is $u(t) = 3 \cos(2t-60^{\circ}) + 4 \cos(4t+30^{\circ}) + 7 \cos(6t+45^{\circ})$. The system frequency response is given by the piecewise function:

$$H{j \omega} = \begin{cases} 0, & 0 < \omega < 3 \\ 1, & 3 \leq \omega \leq 5 \\ 0, & \omega > 5 \end{cases} $$

In previous sections, we used the frequency response of a system to determine the system output, when the input to the system consists of signals comprised of one or more sinusoidal components. This analysis approach is extremely powerful, since it turns out that nearly any signal can be represented as a superposition of sinusoids¹⁾. We will ultimately, therefore, use our frequency domain analysis approaches on a very broad range of input signals, many of which may have very little resemblance to sinusoidal signals.

Often, a graphical representation of the system’s frequency response and the frequency content of the signals of interest can facilitate analysis and provide insight into the overall system behavior. We have seen an example of this in example 10.3. In this chapter, we introduce the concept of a signal’s spectrum – the frequency content of a signal – and we will look more closely at the representation of frequency responses in graphical form. We will conclude this section with an example of the use of signal spectra and frequency response plots to obtain a qualitative representation of a system’s frequency domain response to some input.

The signals currently of interest to us are sinusoidal. Any sinusoidal signal can be written in the form:

$$f(t) = A \cos(\omega_0 t + \theta) (Eq. 11.3)$$

The signal is completely defined by its amplitude, A, its frequency, $\omega_0$, and its phase angle, $\theta$. Our primary interest in these signals is as inputs and outputs to systems. As indicated in section 10.1, we can characterize systems by their magnitude and phase responses as functions of frequency. To be consistent with this frame of mind, we will consider sinusoidal signals of the type shown in equation (11.3) to be functions of frequency as well. We will thus begin to consider the frequency, $\omega$, to be an independent variable, much in the same way that time was treated as an independent variable when we determined time domain responses of first and second order systems.

With frequency treated as an independent variable, the sinusoidal signal of equation (11.3) can be re-written in terms of $\omega$:

$$F{j \omega} = \begin{cases} A \angle \theta, & \omega = \omega_0 \\ 0, & \text{otherwise} \end{cases} (Eq. 11.4) $$

The frequency domain representation of a sinusoidal signal has two dependent variables: the amplitude and the phase. Our immediate goal is to represent the frequency content of signals graphically – we will, therefore, need to use two plots: amplitude as a function of frequency and phase as a function of frequency.

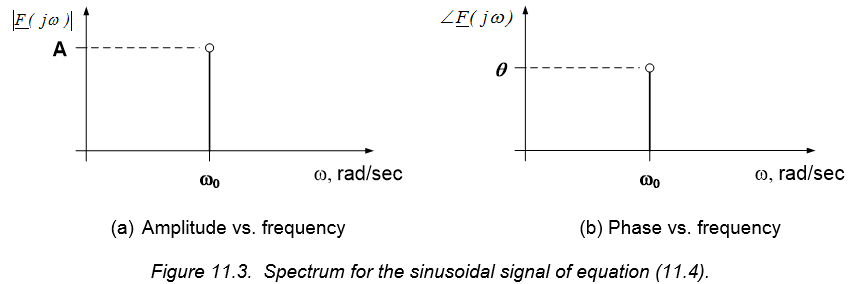
A signal’s amplitude and phase as functions of frequency is called the spectrum of the signal. If we are provided with the spectrum of the signal, we have all the information necessary to completely define the signal. Signal spectra are often presented graphically in terms of two plots; we will refer to the plot of amplitude as a function of frequency as the magnitude spectrum, while the plot of phase as a function of frequency will be called the phase spectrum. As an example, the magnitude and phase spectra of the signal provided in equation (11.4) are shown in Figure 11.3 below.

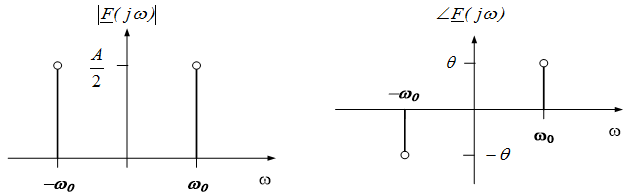
• The term spectrum is most commonly applied to the plot of amplitude and phase vs. frequency of signals in complex exponential form. For example, the signal of equation (11.1) can be written in terms of complex exponentials as: $f(t)= \frac{Ae^{j(\omega_0 t+ \theta)} + Ae^{-j(\omega_0 t + \theta)}}{2} = \frac{A}{2}e^{j \theta} e^{j \omega_0 t} + \frac{A}{2}e^{-j \theta} e^{-j \omega_0 t}$. The spectral plot of the signal in this form is shown below. Note that spectra in this form have both positive and negative frequencies. In our discussions in this chapter, we will present spectra only in terms of having positive frequencies.

• The time domain representation of a signal has only one dependent variable – the value of the signal at any time. Time domain representations are therefore represented graphically as a single plot with time on the horizontal axis. This difference is, fundamentally, due to the fact that we do not work with complex functions of time; if we could measure a signal with both real and imaginary parts, two plots would be required.)

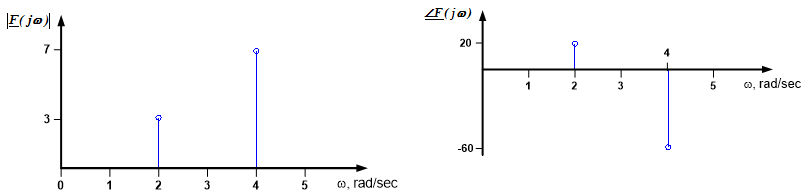
Plot the spectrum of the voltage signal $v_{in}(t) = 3 \cos(2t+20^{\circ}) + 7cos(4t-60^{\circ})$. (Note: this is the same signal as that used in Example 10.20; for a time-domain plot of the signal, see that example.)

The phasor form of this signal can be expressed as a function of frequency as:

$$\underline{V}_{in}(j \omega) = \begin{cases} 3 \angle 20^{\circ}, & \omega=2 \text{rad/sec} \\ 7 \angle -60^{\circ}, & \omega=4 \text{rad/sec} \\ 0, & \text{otherwise} \end{cases} $$

The spectrum is shown below:

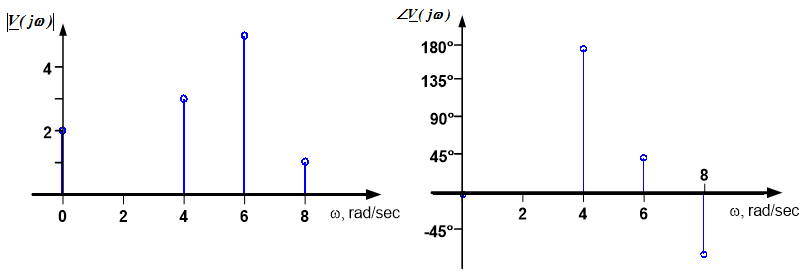
Plot the voltage signal $v(t) = 2 - 3 \cos(4t) + 5 \cos(6t+45^{\circ}) + \cos(8t-75^{\circ})$ and its spectrum.

A plot of the time domain signal is shown below.

A couple of notes should be made about the spectrum of this signal. (1) The constant (DC) value of two corresponds to a frequency of zero rad/sec, since we can write $2 = 2 \cos(0t)$. (2) Sinusoidal amplitudes are by definition positive, so the negative sign in the $-3 \cos(4t)$ term must be accounted for in the phase. Therefore, we re- write this term as $+3 \cos(4t+180^{\circ})$. The spectrum of the signal can then be plotted as shown below:

We have previously seen that the frequency response of a system consists of the system’s magnitude response and phase response. The magnitude response provides the gain of the system (the ratio between the amplitudes of the output and input sinusoids) as a function of frequency, while the phase response provides the change in phase between the input and output sinusoids, as a function of frequency. In this section, we will emphasize the presentation of this information graphically. We do this by plotting the frequency response of two simple first order circuits in the examples below.

Plot the frequency response for the circuit shown below. The voltage $v_{in}(t)$ is the input and the capacitor voltage $v_{out}(t)$ is the desired response.

A mathematical expression for the frequency response of this circuit was determined in example 11.1 to be:

$$H(j \omega) = \frac{2}{2+ j \omega}$$

The magnitude and phase responses, as functions of frequency are, therefore:

$$|H(j \omega)| \frac{2}{\sqrt{4+\omega^2}}$$

And:

$$\angle H(j \omega) = =\tan^{-1}(\frac{\omega}{2})$$

Plotting these functions results in the graphical frequency response shown below:

Plot the frequency response for the circuit shown to the left below. The source voltage $v_S(t)$ is the input and the inductor voltage $v(t)$ is the output.

We begin by converting the circuit to the frequency domain. Representing the input and output signals as phasors and the circuit elements as impedances results in the circuit to the right above. This circuit suggests that the output voltage can be determined from the input voltage via a voltage divider formula:

$$\underline{V} = \frac{j2 \omega}{1+j2 \omega} \cdot \underline{V}_S$$

The circuit frequency response, $H(j \omega)$, is the ratio of the output phasor to the input phasor:

$$H(j \omega) = \frac{\underline{V}}{\underline{V}_S} = \frac{j2 \omega}{1+j2 \omega}$$

So that the magnitude and phase response of the circuit are:

$$|H(j \omega)| = \frac{2 \omega}{\sqrt{1^2 + (2 \omega)^2}}$$

And:

$$\angle H(j \omega) = 90^{\circ} - \tan^{-1}(2 \omega)$$