When we think of chaos, we tend to picture a mini-van full of hungry kids or that one tenured professors’ dark, graduate student-infested office. But in reality, pure chaos is an intrinsic part of our world.
Technologies that helps us gather information and explain the world around us are arguably among the most important developments. And also, come on… one must admit that chaos theory is pretty cool. So, leave your thoughts of sad offices and mini-vans behind!
(Unless they actually include hungry children, in which case perhaps don’t).
Scientifically, chaotic behavior in waveforms can be defined, simply, as a wave that never repeats. With a simple non-linear circuit, function generator, and an oscilloscope, we can create waveforms that extend into chaos.
But alas, you say oscilloscopes and function generators are bulky, beige and expensive? Fear not!

Digilent’s Analog Discovery 2 is the pocket sized equivalent of both an oscilloscope and a function generator, plus a ton of other cool stuff (which you can read about more in depth by clicking here).
By downloading Waveforms, an easy to use waveform analyzer software, we can use the Analog Discovery 2 like we would an oscilloscope. All we have to do is hook it up to our computer.
Our simple non-linear circuit is called Chua’s circuit, conveniently named after the guy who invented it. Click here for a step-by-step run through on how to build one.
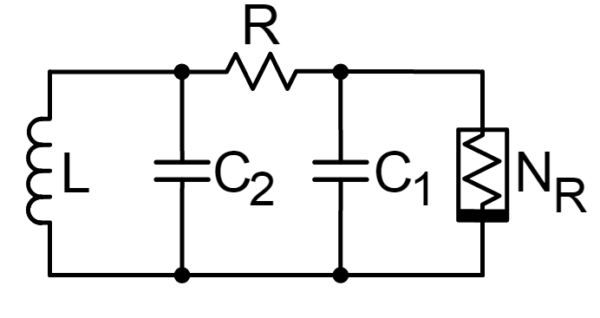 Chua circuit diagram (Wikipedia)
Chua circuit diagram (Wikipedia)
We can also run the Analog Discovery 2 as both a function generator and a 2-channel oscilloscope simultaneously…which is nothing short of GENIUS!
Head over to our Wiki to see how.
If we run a continuous sine wave across the circuit using the function generator, we see a sine wave as the output of the circuit on the oscilloscope. As we increase the voltage, the period of our sine waves double, quadruple, and all of the sudden the waveform goes chaotic.
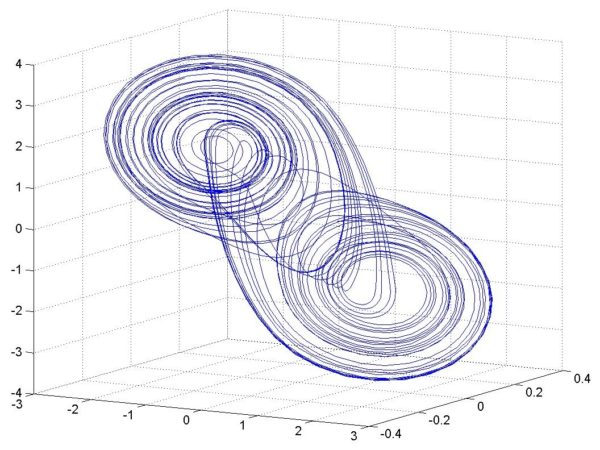
An example of chaotic behavior modeled in 3D (Wikipedia)
What the heck is happening?
Technically, quantum bifurcation. Less technically, the high voltage is forcing the period of our sine wave to halve each time the voltage is increased. A tipping point is reached once the period can’t be halved anymore, and the result is chaos.
Taking a perfectly-content sine wave and forcing it into chaos sounds a little dismal, so why would we ever want to do this? Well, applications of understanding and replicating chaotic behavior range from helping predict heart attacks to more secure cryptography.
Want to see what else we’re doing with the Analog Discovery 2 and other cool projects? Subscribe to our newsletter and stay up to date on our blog!


You know you’ve taken way too many math classes when you know what a quantum bifurcation is without clicking on the link. Super fun class to learn about chaos, gritty homework involving many drawings of vector maps not so much.
Interesting post! Do you know exactly what is happening in terms of physics when the period “can’t be halved anymore?”
Hi Talesa,
Chaos, in mathematics, is where a set of differential equations with a set of initial conditions are plotted over time and eventually the result from solving the differential equations becomes erratic and non-repeating. This behavior results from what is known as a bifurcation – essentially a point where a trajectory splits off into different directions. Ideally, when working with such sets of equations, both your equations and initial conditions are perfect and precise so you would be able to calculate the behavior of your model out to infinite time.
However, computers have limited precision and more complex equations generally require a fourier transformation to be performed on the equations to make them solvable via methods such as 4th order Runge-Kutta or Newton iteration, but the farther out you go (in iterations) the more complex the equation to solve becomes and eventually the result begins to deviate wildly – chaos. This phenomena is the same reason why we can only predict the weather a few days in advance, our equations and initial conditions are not accurate or precise enough to predict farther out into the future.
As for why this happens in the Chua’s circuit (as I learned from this site: https://courses.physics.illinois.edu/phys406/Student_Projects/Fall00/MChukhman_NSears/chua_index.html) is that it contains a locally active resistor which apparently has negative resistance and can actually amplify and provide power to generate the oscillating circuit. But because this circuit is a feedback loop and the amplification that occurs is non-linear, a new output is produced and eventually errors in measurement add up producing the chaotic behavior.
I guess one point I do want to clarify is that this chaotic nature only “exists” in the mathematical models. If you looked at your circuit at one point it’ll be predictable up to a point, but if you then redid all of your initial conditions after this point where the chaotic behavior started to occur, it would no longer be there at that particular point in time, but would eventually become chaotic again (in the math model) in the future. Going back to the weather predictions, that’s basically what they do there, get a new set of initial conditions so that they can get the most accurate (i.e. least amount of accumulated errors) for the weather occurring “next”.
Ella, please feel free to correct me if I got any of this wrong; it’s been awhile since I’ve worked with this.
Hi James,
Applying chaos in cryptography is my research area, you can put in google Merah Lahcene chaos FPGA, you can find a lot of experimental implementations of such systems using only DIGILENT products.