Lab 2: Active and Passive Filters
This lab introduces students to the basic terminology and characteristics of filters such as filter slope, passband, stopband, and cut-off frequency. Students will learn about filter transfer functions for passive and active filters as well as higher-order passive filters and apply their knowledge by simulating and building these circuits. Advanced students can challenge themselves by exploring higher-order active filter implementations (such as Chebyshev and Butterworth) and how these implementations maximize different filter characteristics.
Introduction
In the first lab you were introduced to the basic RC filter, however, we did not discuss the filter characteristics. Filter circuits play an important role in many electronics designs. They are primarily used to pass desired signals while blocking unwanted signals. Filters can be divided into two main categories, analog and digital filters, and each category can be further divided into many sub-groups, such as passive filters, active filters, FIR filters, or IIR filters. Each sub-group of filters has their own advantages and disadvantages. Learning the difference between each filter will allow a filter design engineer to choose the best type of filter for a given application.
Going through every filter type would be too time consuming for a single lab. To narrow our focus, in this lab we will use analog filters to introduce basic filter characteristics and design. We will also talk about the difference between passive filters and active filters and how they can affect design choices.
Learning Objectives
In this section, students will:
- Simulate an RC passive filter
- Build an active filter using an operational amplifier
Part List
The following equipment is required for this experiment:
Hardware
- 1μF electrolytic capacitor
- 0.1μF ceramic capacitor
- 10KΩ resistor
- 2x 1KΩ resistor
- OP27, or compatible operational amplifier
Software
Circuit Theory and Simulation
Passive Filter
Passive filters are filters that consist of only passive components such as resistors, capacitors, and inductors (RLC). For low frequency applications, RC filters are used since an inductor’s physical size can be very large for low frequency applications. As operating frequency increases, the inductor size can be smaller making it a good choice for RF applications that operate in the MHz range. In this section, you will work with the RC filter but the concepts you learn also apply to both RL and RLC filters.
The RC low-pass filter characteristics are:
- Pass band – frequency range where the input frequency is not attenuated compared to the output.
- Stop band – frequency range where the input signal begins to be attenuated.
- Cutoff frequency – the transition boundary between the pass band and stop band, this is when Vout is 1√2 of Vin or 0.0707. On decibel scale the value is at -3dB.
- Slope – the slope determines how fast the signal is attenuated after the cutoff frequency. The slope is a main consideration a designer takes into account when building a filter.
- Phase shift – is the phase difference between the input and output signal.
- y-axis – is the amplitude of the signal expressed in decibels (dB).
- x-axis – frequency, expressed on a logarithmic scale.
Now that the filter characteristics have been defined, lets investigate how to obtain these values mathematically.
In the s-domain, the capacitor impedance is defined as: $X_C=\frac{1}{sC}$,
where $s=j\omega$ or $s=j2{\pi}f$ and j represents the complex number. A resistor in the s-domain is just its resistance value. The transfer function is often used to define the filter characteristic, this is simply the output signal divided by the input: $H(s)=\frac{V_{out}(s)}{V_{in}(s)}$
For an RC filter, you can use the voltage divider rule to find the output signal: $V_{out}=\frac{X_C}{R+X_C}V_{in}$
If we substitute Xc and R with their s-domain representation and then rearrange, the RC transfer function is: $H(s)=\frac{\frac{1}{Cs}}{R+\frac{1}{Cs}}=\frac{1}{sRC+1}$
Substituting jω for s, the transfer functions becomes: $H({\omega})=\frac{1}{j{\omega}RC+1}$
The AC Sweep analysis in Multisim shows the filter response in terms of magnitude vs frequency, therefore, expressing the transfer function as magnitude will be helpful. The magnitude of the transfer function can be calculated as: $|H({\omega})|=\frac{1}{\sqrt{({\omega}RC)^2+1}}$
The second graph from the AC Sweep Analysis represents phase difference between the input and output. We can calculate the angle using the formula: ${\theta}=-arctan({\omega}RC)$
Often the filter response is expressed as decibel gain and it is given by the following equation: $A(s)=-20log(\frac{V_{out}}{V_{in}})[dB]$
The cutoff frequency of a filter is at the -3 dB point. For an RC filter this occurs when $X_C$ is equal to R: $R=X_C=\frac{1}{2{\pi}f_{c}C}$ → $f_c=\frac{1}{2{\pi}RC}$, where $f_c$ is the cut-off frequency.
In many filter applications, the filter slope after the cut-off frequency is an important design specification. This specification is expressed as dB/decade. For a passive RC filter, the filter slope is constant, regardless of what resistor and capacitor values you use.
- Questions and Exercises
-
- Design a filter with a cut-off frequency of 1kHz. Verify your design by using Multisim. What resistor and capacitor did you use?
- Build the low-pass filter from Lab 1: Resistor-Capacitor Circuits using Multisim and then run the AC Sweep analysis. Determine the output magnitude and phase when the input frequency is: 1Hz, 10Hz, 100Hz, 1kHz, and 100kHz. Compare your calculation with the simulation results.
- Set the Grapher vertical scale to Logarithmic and keep the horizontal scale as Decade in Multisim Live (these settings are accessible through the Configuration Pane in the Grapher window). Note that a decade is a factor of 10 difference between two numbers. For example, 1 to 10 is one decade and 10 to 100 is another decade. What is the slope of the RC filter expressed as dB/decade?
Filter Order
The RC filter you just analyzed is a $1^{st}$ order filter and you can see the slope is gradual. To design a filter closer to an ideal filter, which has a sharp drop pass the cut-off frequency, you have to increase the filter order. One easy way to increase the filter order of RC filters is to cascade multiple RC low-pass filters into a ladder network.
Each additional resistor-capacitor pair you add increases the filter order by 1.
To derive the transfer function of the above circuit, you can use Kirchhoff’s Current Law:
$\frac{V_1-V_{in}}{R_1}+\frac{V_1-V_{out}}{R_2}+sC_1V=0$
$\frac{V_{out}-V_{in}}{R_2}+sC_2V_{out}=0$
Rearranging the equations, we can get the transfer function: $H(s)=\frac{1}{s^2R_1R_2C_1C_2+s(R_1C_1+R_1C_2+R_2C_2)+1}$
- Questions and Exercises
-
- Build the circuit in Multisim and compare the slopes of the $1^{st}$ order and $2^{nd}$ order filters.
Active Filter
As we’ve seen, passive filters are easy to configure and design. This makes the passive filter viable in many applications, but there are some drawbacks. For example, if the load impedance changes, it will cause the frequency response to change making it difficult to control for systems that have variable load impedances. This is where the active filter comes in. An active filter has an active component, usually an opamp. Because the active filter has an opamp, we can also design the filter to have high input impedance and low output impedance. With this configuration, the load will have little impact on the frequency response.
In addition to providing a buffer that limits the effect of load impedance, an active filter also allows us to add gain into the filter circuitry. The image on the right shows an active low-pass filter configuration using an opamp.
The transfer function for the circuit above is given by: $H(s)=\frac{-R_2}{R_1}(\frac{1}{R_2C_1s+1})$
The magnitude for the transfer function is given by: $|H(s)|=\frac{R_2}{R_1}\frac{1}{sqrt{(R_2C_1{\omega})^2+1}}$
The phase angle is given by: ${\phi}H(s)=180-arctan(R_2C_1{\omega})$
The gain is taken when frequency is zero and it is the ratio between: $A=-\frac{R_2}{R_1}$
You can set the filter roll off frequency as follows: $f_c=\frac{1}{2{\pi}R_2C_1}$
- Questions and Exercises
-
- Find the magnitude of the filter for the following frequency: 1Hz, 10Hz, 1kHz and 10KHz.
- Design a filter with a gain of 3 that have a cutoff frequency at 1kHz. Use Multisim to simulate your design. What resistor and capacitor values did you use?
Building and Measuring Your Circuit
In the first lab, an RC filter was built and you used the scope to view the output signal as you increased the Function Generator frequency. You also used the Network Analyzer to view the response in the frequency domain. For this lab, the input signal is a sine wave with noise and you will use the RC filter to remove the noise from the signal.
Passive Filter
Connect one pin of the resistor to the W1 pin of the signal generator, the other to the positive pin of the capacitor. Connect the negative pin of the capacitor to the grounded pin of the signal generator. Connect the second Scope Channel 2+ (blue wire) to the junction between the resistor and capacitor, then the Scope Channel 2- (blue-white wire) to the negative pin of the capacitor. Connect the first Scope Channel 1+ (orange wire) to the signal generator's W1 pin (yellow wire) and the Scope Channel 1- (orange-white wire) to the negative pin of the capacitor (this pin is grounded).
Don't forget to turn the Scope Channel 1 and 2 switches towards the MTE headers.
You can download the wiring diagram here: wiring_diagram_fr.zip
Launch WaveForms and open the Wavegen instrument, then select Custom and then click New. In the Math tab enter the following relation: $sin(2*PI*X)+0.1*sin(30*PI*X)$, which will generate the following signal: $V(t)=sin(2{\pi}ft)+0.1sin(30{\pi}ft)$, where $sin(2{\pi}ft)$ is the input signal and $0.1sin(30{\pi}ft)$ is the noise at a frequency 15 times higher than the input signal.
Click on Generate.
Set the frequency to 10Hz and start the instrument. Use the Scope to view the circuit response in the time domain.
- Questions and Exercises
-
- Was the noise removed from the circuit?
- Compare the phase difference between the input signal with the output signal. How does it compare to your previous calculations at 100Hz? Keep in mind the tolerance of the electrolytic capacitor is ±20%.
- Connect the output of your filter in series with a 1kΩ resistor. In this situation, the resistor simulates a load that we have connected to the filter. How does the load resistance affect the circuit output? What if you used a 100Ω resistor?
Active Filter
Build the circuit presented in Active Filter on the Breadboard Canvas. You will need to power the opamp with ±5V, from the variable power supply (red and white wires). Connect the function generator's W1 channel (yellow wire) and the oscilloscope's Channel 1+ (orange wire) to the input of the circuit and the 2+ channel of the oscilloscope (blue wire) to the output of the circuit. Connect to the ground the 1- and 2- channels of the oscilloscope (orange-white and blue-white wires), the function generator's ground and the positive input of the opamp.
Don't forget to turn the Scope Channel 1 and Scope Channel 2 switches towards the MTE headers and the V+ switch towards the POWER inscription.
You can download the wiring diagram here: wiring_diagram_active.zip
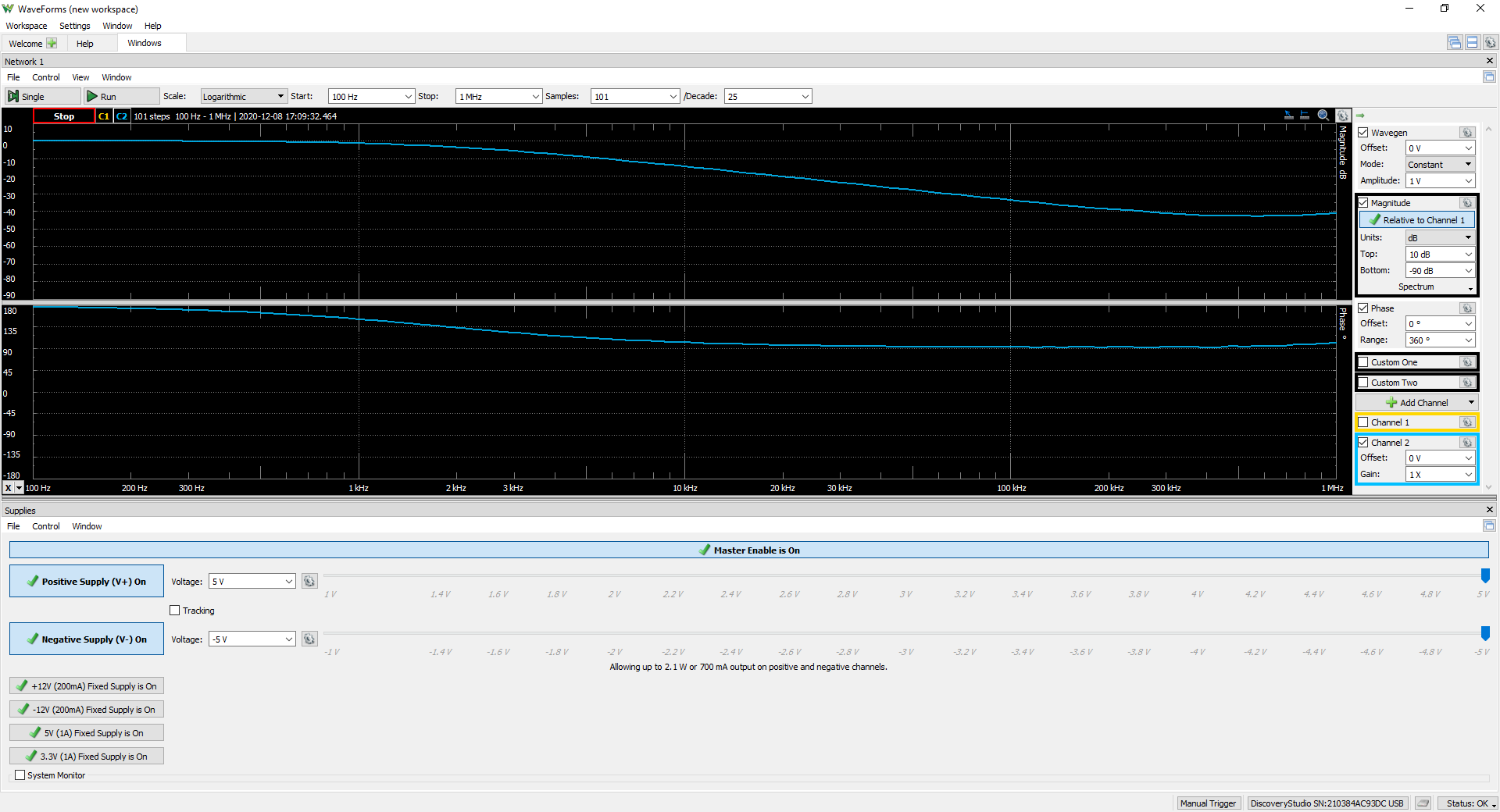
In WaveForms start the Supplies instrument, set the voltages to +5V and -5V and turn on the master enable to power the IC. In the Wavegen instrument set the previously presented noisy sinusoidal signal and set the frequency to 500Hz. Use the Scope to view the circuit response in the time domain.
- Questions and Exercises
-
- How does the response from the Analog Discovery Studio compare to the simulation?
- Design an active filter with gain of 2 and a cutoff frequency of 1kHz. What are the values of resistors and capacitors needed to meet the design specifications?
- Connect the output of your filter in series with a 1kΩ resistor. In this situation, the resistor simulates a load that we have connected to the filter. How does the load resistance affect the circuit output? What if you used a 100Ω resistor?
Further Exploration
The section below provides a way to continue exploring after finishing the lab. It covers multiple orders in active filters and different types of filter responses.
Higher-Order Active Filters
In this lab we had talked about how to make higher-order passive filters in order to increase the slope roll-off. When discussing higher-order active filters there are actually several common filter transfer function solutions that have been developed over the years, with each solution maximizing different aspects of the filter. Two common examples of these solutions are the Butterworth and the Chebyshev solutions.
Open the circuits in Multisim and compare the Butterworth and Chebyshev filter implementations. Since they use the same circuit architecture, how do the two designs differ? Perform an AC analysis on the two filter circuits. How does the frequency response of the Butterworth filter differ from the frequency response of the Chebyshev filter?
Both filters were designed to have a cut-off frequency at 1kHz. The ideal filter response would be a “brick wall” that is flat in the passband and has an immediate vertical drop at the cut-off frequency. How do the two frequency responses differ from the ideal? When might you choose to use one over the other?
Next Steps
For more complementary laboratories, return to the Complementary Labs for Electrical Engineering page of this wiki.
For technical support, please visit the Test and Measurement section of the Digilent Forums.