Real Analog: Chapter 8
- Chapter 8 Materials
-
- Lecture Material:
- Lecture 20(b) PowerPoint Slides: First-order circuit step response, introduction to second-order systems
- Lecture 21 PowerPoint Slides: Second-order circuit natural response, sinusoidal signals & complex exponentials
- Lecture 22 PowerPoint Slides: Second-order system natural response, mathematical form of solutions, qualitative interpretation
- Lecture 23 PowerPoint Slides: Second-order system step response, governing equation, mathematical expression, estimating step response, examples
- Chapter 8 Video:
- Lab 8 Video 1: Second Order Circuit Step Response: Measuring the step response of a series RLC circuit. The measured peak value of the response is compared to analytical expectations.
-
-
- Exercise Solutions: Chapter 8 exercise solutions
- Homework: Chapter 8 homework problems
8. Introduction and Chapter Objectives
Second order systems are, by definition, systems whose input-output relationship is a second order differential equation. A second order differential equation contains a second order derivative but no derivative higher than second order. Second order systems contain two independent energy storage elements, per our comments in Chapter 7 pertaining to the relationship between the number of energy storage elements in a system and the system order
Second order systems, like first order systems, are an extremely important class of systems. In previous chapters, we saw that the natural response of first order systems decays exponentially with time – the natural response decays monotonically to zero. The natural response of second order systems can, however, oscillate with time – we will see that a second order systems response can contain sinusoidal components. The motion of a pendulum, for example, can be modeled by a second order system. These oscillations are due to the transfer of energy between the two energy storage mechanisms; a pendulum, for example, oscillates because of the cyclic exchange of potential and kinetic energy of the mass.
Since the natural response of second-order systems can oscillate with time, their response can be fundamentally different than the response of first order systems. In the introduction to chapter 7, we noted that it is common to approximate higher-order systems as first order systems (at the time, we said that such a system has dominant first order modes). This approximation is not possible if the natural response of the higher order system oscillates. However, it may be possible to approximate the response of such a system as a second order system. Systems which behave approximately as second order systems have what are called dominant second order modes. In fact, the natural response of any higher order system can be considered in terms of the responses of multiple first and/or second order systems1). This is why an understanding of first and second order system responses is so crucial to the engineer – these responses provide the building blocks for understanding the responses of all linear systems.
In this textbook, of course, we are interested in the response of electrical circuits. Thus, we begin this chapter with a presentation of two simple second order electrical circuits: the series RLC and parallel RLC circuits. In section 8.1, we derive the governing equations for these circuits and use the results to write the general form of the differential equation governing second order systems. This equation is in terms of two very important parameters: the system natural frequency and the system damping ratio. The homogeneous solution of this general equation is determined in sections 8.2 and 8.4. In section 8.2, we develop the form of the solution (in terms of the natural frequency and damping ratio). Since the response of second order systems contains complex exponential functions, we provide some material (in section 8.3) relative to complex exponentials and sinusoidal signals. This material will provide us the necessary background to allow us to determine the natural response. Section 8.3 is optional for readers who are comfortable with complex exponential and sinusoidal signals. The overall natural response is developed in section 8.4, using the solution form presented in section 8.2 and the background material on complex exponentials in section 8.3.
After Completing this Chapter, You Should be Able to:
- Write differential equations governing second order circuits
- Define damping ratio and natural frequency from the coefficients of a second order differential equation
- Express the form of the natural response of an arbitrary second order system in terms of complex exponentials, the damping ratio, and the natural frequency
- Summarize the behavior of the complex exponentials in the system natural response for the damping ratio ranges below:
- Damping ratio greater than one
- Damping ratio less than one
- Damping ratio equal to one
- Write complex numbers in terms of complex exponentials
- Express sinusoidal signals in terms of complex exponentials
- Classify overdamped, underdamped, and critically damped systems according to their damping ratio
- Identify the expected shape of the natural response of over-, under-, and critically damped systems
- State from memory the definition of an underdamped second order system’s overshoot, rise time, and steady-state response
- Use the coefficients of a second order system’s governing equation to estimate the system’s overshoot, rise time, and steady-state response
8.1: Introduction to Second Order Systems
We will develop our discussion of second order systems in the context of two electrical circuits examples.
Example 8.1: Series RLC Circuit
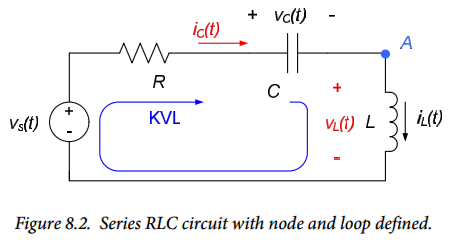
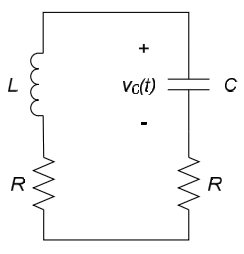
Consider the circuit shown in Figure 8.1 below, consisting of a resistor, a capacitor, and an inductor (this type of circuit is commonly called an RLC circuit). The circuit contains two energy storage elements: an inductor and a capacitor. The energy storage elements are independent, since there is no way to combine them to form a single equivalent energy storage element. Thus, we expect the governing equation for the circuit to be a second order differential equation. We will develop equations governing both the capacitor voltage, $v_C(t)$ and the inductor current, $i_L(t)$ as indicated in Figure 8.1.
In order to determine the governing equations for $v_C(t)$ and $i_L(t)$ we will attempt to write two first-order differential equations for the system and then combine these equations to obtain the desired second order differential equation. To facilitate this process, the circuit of Figure 8.1 is repeated in Figure 8.2 with the node and loop we will use labeled. Note that we also label the current through the capacitor in terms of the capacitor voltage and the voltage across the inductor in terms of the inductor current.
The voltage-current relationships for inductors and capacitors indicate that, in Figure 8.2, $i_C(t)=C\frac{dv_C(t)}{dt}$ and $v_L(t)=L\frac{di_L(t)}{dt}$. Using the latter of these relations, KVL around the indicated loop in Figure 8.2 provides:
$$v_s(t)=Ri_L(t)+v_C(t)+L\frac{di_L}{dt} (Eq. 8.1)$$
KCL at node A, along with the voltage-current relation for the capacitor, indicates that:
$$C\frac{dv_C(t)}{dt}=i_L(t) (Eq. 8.2)$$
We can determine the equation governing the capacitor voltage by differentiating equation (8.2) with respect to time to obtain an expression for the derivative of the inductor current:
$$C\frac{d^2v_C(t)}{dt^2}=\frac{di_L(t)}{dt} (Eq. 8.3)$$
Substituting equations (8.2) and (8.3) into equation (8.1) results in:
$$v_S(t)=RC\frac{dv_C(t)}{dt}+v_C(t)+LC\frac{d^2v_C(t)}{dt^2}$$
Rearranging this slightly results in:
$$\frac{d^2v_C(t)}{dt^2}+\frac{R}{L} \frac{dv_C(t)}{dt}+ \frac{1}{LC} v_C(t) = \frac{1}{LC}v_S(t) (Eq. 8.4)$$
To determine the relationship governing the inductor current, we can again use equation (8.2) to write the capacitor voltage as:
$$v_C(t) = \frac{1}{C} \int_{0}^{t} i_L(t)dt (Eq. 8.5)$$
Where we assume that the voltage across the capacitor at time $t = 0$ is zero; e.g. $v_C(0) = 0$.
Substituting equation (8.5) into equation (8.1) results in the integro-differential equation:
$$v_s(t)=Ri_L(t) + \frac{1}{C} \int_{0}^{t} i_L(t)dt + L \frac{di_L}{dt}$$
In general, we prefer not to work with a mixture of derivatives and integrals in the same equation, so we differentiate the above to obtain our final expression for $i_L(t)$:
$$\frac{d^2i_L(t)}{dt^2}+\frac{R}{L} \frac{di_L(t)}{dt} + \frac{1}{LC}i_L(t) = \frac{1}{L} \frac{dv_S(t)}{dt} (Eq. 8.6)$$
Important Tip:
Equations (8.1) and (8.2) consist of two coupled first order differential equations in two unknowns: $i_L(t)$ and $v_C(t)$. This set of differential equations completely describes the behavior of the circuit – if we are given appropriate initial conditions and the input function $v_S(t)$ they can be solved to determine the inductor currents and capacitor voltages. Once the capacitor voltage and inductor current are known, the energy in the system is completely defined and we can determine any other desired circuit parameters. Any manipulations of equations (8.1) and (8.2) we performed subsequently do not fundamentally increase the information we have about the circuit – we were simply rearranging equations (8.1) and (8.2) to create a single equation with the desired unknown.
Example 8.2: Parallel RLC Circuit
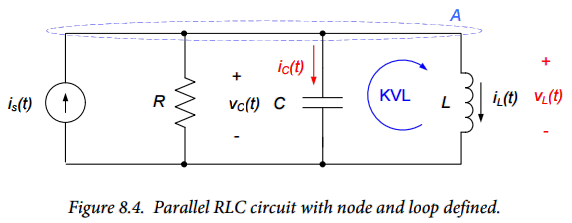
Our second exemplary circuit is the parallel combination of a resistor, capacitor, and inductor shown in Figure 8.3. The circuit is, for relatively obvious reasons, called a parallel RLC circuit. The forcing function to the circuit is provided by a current source, $i_S(t)$. The circuit of Figure 8.3, like that of Figure 8.2, contains two independent energy storage elements –we expect the governing equations for the circuit to be second order differential equations. We will again develop equations governing both the capacitor voltage, $v_C(t)$ and the inductor current, $i_L(t)$ as indicated in Figure 8.3.
Consistent with our approach for the series RLC circuit, we will write first order differential equations using the variables $v_C(t)$ and $i_L(t)$ and subsequently combine these equations to eliminate the undesired unknown. Figure 8.4 shows the node and loop we will use to generate these equations. Figure 8.4 also shows the current through the capacitor in terms of the capacitor voltage and the voltage across the inductor in terms of the inductor current.
KVL around the indicated loop provides:
$$L\frac{di_L(t)}{dt}=v_C(t) (Eq. 8.7)$$
KCL at node A provides:
$$i_S(t)=\frac{v_C(t)}{R}+i_L(t)+C\frac{dv_C(t)}{dt} (Eq. 8.8)$$
As in example 8.1, equations (8.7) and (8.8) completely describe the circuit’s response. However, to gain additional insight into the individual parameters $v_C(t)$ and $i_L(t)$, we rearrange these equations into second order differential equations in a single dependent variable. For example, we can differentiate equation (8.7) to obtain:
$$L\frac{d^2i_L(t)}{dt^2}=\frac{dv_C(t)}{dt} (Eq. 8.9)$$
Equations (8.7) and (8.9) can be substituted into equation (8.8) to obtain a second order differential equation in the variable $i_L(t)$. After some manipulation, the resulting equation is:
$$\frac{d^2i_L(t)}{dt^2}+\frac{1}{RC} \frac{di_L(t)}{dt} + \frac{1}{LC} i_L(t) = \frac{1}{LC}i_S(t) (Eq. 8.10)$$
Likewise, we can integrate equation (8.7) and use the result to write equation (8.8) in terms of the capacitor voltage:
$$\frac{d^2v_C(t)}{dt^2} + \frac{1}{RC} \frac{dv_C(t)}{dt} + \frac{1}{LC} v_C(t) = \frac{1}{C} \frac{dv_S(t)}{dt} (Eq. 8.11)$$
The important thing to note about the above examples is that equations (8.4), (8.6), (8.10), and (8.11) can all be written in the form:
$$\frac{d^2y(t)}{dt^2}+2 \zeta \omega_n \frac{dy(t)}{dt} + \omega_{n}^{2}y(t)=f(t) (Eq. 8.12)$$
Where $y(t)$ is the system parameter of interest (for example, a voltage or current in an electrical circuit), $\omega_n$ is the undamped natural frequency and $\zeta$ is the damping ratio; the physical significance of these parameters will be presented later in this series of chapters. The point being made here is that the governing equation for any second order system can be written in the form of equation (8.12); thus, we will focus on this format for our discussion of the solution of second order differential equations.
Section Summary
- Second order systems have two independent energy storage elements. These circuits are governed by second order differential equations.
- Unlike first order circuits, the natural response of second order circuits can oscillate. This oscillation is due to energy exchanges between the two energy storage elements (inductors and/or capacitors, in electrical circuits). The oscillations will die out with time due to energy dissipation elements (resistors, in electrical circuits).
- The general differential equation governing second order circuits is of the form:
$$\frac{d^2y(t)}{dt^2} + 2 \zeta \omega_n \frac{dy(t)}{dt} + \omega_{n}^{2} y(t) = d(t)$$
where $y(t)$ is a voltage or current of interest in the circuit.
- In the equation above, $\omega_n$ is called the undamped natural frequency and $\zeta$ is called the damping ratio. These parameters (along with the DC gain of the circuit, as presented in section 7.5) govern the shape of the circuit natural response.
Exercises
1. The differential equation governing a circuit's natural response is:
$$\frac{d^2y(t)}{dt^2} + 32 \frac{dy(t)}{dt} + 64y(t) = 0$$
Where $y(t)$ is the circuit response. What are:
- The circuit's natural frequency and,
- The circuit's damping ratio
2. The differential equation governing a circuit's natural response is:
$$\frac{d^2y(t)}{dt^2} + 8 \frac{dy(t)}{dt} + 64y(t) = 0$$
Where $y(t)$ is the circuit response. What are:
- The circuit's natural frequency and,
- The circuit's damping ratio
3. For the circuit below, determine the differential equation for $i_L(t), t>0$. (Hint: write KCL at node A and KVL around loop 1 to get two equations in two unknowns, $v_c(t)$ and $i_L(t)$. Then combine the equations to eliminate $v_c(t)$.)
4. For the circuit shown below, apply KCL at node A and KVL around loop 1 to write two first order differential equations in two unknowns: the current through the inductor and the voltage across the capacitor. Combine these equations to write a single second order differential equation in the voltage $v(t)$.
8.2: Second Order System Natural Response - Part 1
In section 8.1, we determined that the the differential equation governing a second-order system could be written in the form:
$$\frac{d^2y(t)}{dt^2} + 2 \zeta \omega_n \frac{dy(t)}{dt} + \omega_{n}^{2} y(t) = f(t)$$
Where $y(t)$ is any system parameter of interest (for example, a voltage or current in an electrical circuit), $\omega_n$ and $\zeta$ are the undamped natural frequency and the damping ratio of the system, respectively, and $f(t)$ is a forcing function applied to the system. In general, $f(t)$ is an arbitrary function of the physical input to the system. (The physical input to the system can be, for example, a voltage or current source; $f(t)$ is a function of these power sources. In section 8.1, we saw examples in which $f(t)$ was proportional to an applied voltage or current or proportional to the derivative of an applied voltage or current.)
In this chapter, we will develop the homogeneous solution to the above second order differential equation. For the homogeneous case, the forcing function $f(t)=0$.
In this chapter, we develop the homogeneous solution to the differential equation provided in equation (8.12) of section 8.1. The appropriate differential equation to be solved is thus:
$$\frac{d^2y_h(t)}{dt^2} + 2 \zeta \omega_n \frac{dy_h(t)}{dt} + \omega_{n}^{2}y_h(t)=0 (Eq. 8.13)$$
In equation (8.13), $y_h(t)$ is the solution to the homogeneous, or unforced differential equation given by equation (8.13). A second order differential equation requires two initial conditions in order to solve it; we will take our initial conditions to be the value of the function $y(t)$ at $t = 0$ and the derivative of the function $y(t)$ at $t = 0$. We will state our initial conditions as:
$$y(t=0)=y_0 \\ \frac{dy(t)}{dt} |_{t=0} = y^{'}_{0} \\ (Eq. 8.14)$$
Our approach to the solution of equation (8.13) will be consistent with our previous approach to the solution of first order homogeneous differential equations: we will assume the form of the differential equation (8.13) plug this assumed solution into equation (8.13) and then use our initial conditions to determine any unknown constants in the solution.
Examination of equation (8.13) leads us to conclude that the solution $y_h(t)$ of equation (8.13) must be a function whose form does not change upon differentiation. Thus, we assume (consistent with our approach in section 7.3) that the solution to equation (8.13) will be of the form:
$$y_h(t)=Ke^{st} (Eq. 8.15)$$
Substituting equation (8.15) into equation (8.13) results in:
$$(Ks^2)e^{st} + 2 \zeta \omega_n (Ks)e^{st} + K\omega_{n}^{2}e^{st}=0$$
The above can be simplified to:
$$\left[ s^2 + 2 \zeta \omega_n s + \omega_{n}^{2} \right] Ke^{st} = 0$$
The solutions to the above equation are $Ke^{st}=0$ and $s^2+2 \zeta \omega_ns+\omega_{n}^{2} =0$. The first of these results in the trivial solution, $K = 0$, which in general will not allow us to satisfy our initial conditions. Thus, in our solution given by equation (8.15), we choose s according to:
$$s^2 + 2 \zeta \omega_ns+\omega_{n}^{2} = 0 (Eq. 8.16)$$
Since equation (8.16) is quadratic, values of s which satisfy it are given by:
$$s= \frac{-2 \zeta \omega_n \pm \sqrt{(2 \zeta \omega_n)^2 - 4(2 \zeta \omega_n)\omega_{n}^{2}}}{2}$$
After simplification, this provides:
$$s= - \zeta \omega_n \pm \omega_n \sqrt{\omega^2-1} (Eq. 8.17)$$
Equations (8.15) and (8.17) indicate that there are two possible solutions to equation (8.13). Since the original differential equation is linear, we know that superposition is valid and our overall solution can be a linear combination of the two solutions provided by equations (8.15) and (8.17). Thus, we take our overall solution to be of the form:
$$y_h(t) = K_1e^{s_1t} + K_2e^{s_2t}$$
Where $s_1$ and $s_2$ are provided by equation (8.17) so that:
$$y_h(t) = K_1e^{(-\zeta \omega_n + \omega_n \sqrt{\zeta^2 -1})t} + K_2e^{(-\zeta \omega_n - \omega_n \sqrt{\zeta^2-1})t}$$
Which can be re-written as:
$$y_h(t) = e^{-\zeta \omega_nt} \left[ K_1e^{(\omega_n \sqrt{\zeta^2-1})t} + K_2e^{-(\omega_n \sqrt{\zeta^2-1})t} \right] (Eq. 8.18)$$
The initial conditions, given by equations (8.14) can be used to determine the unknown constants, $K_1$ and $K_2$.
Let us briefly examine the form of equation (8.18) before providing examples of the homogeneous solution for specific circuit-related examples. We do this by examining individual terms in equation (8.18):
- In equation (8.18), the term $e^{- \zeta \omega_n t}$ is an exponential function of the form discussed in section 6.2. Thus, we know that this term corresponds to a decaying exponential, as long as the term $\zeta \omega_n$ is positive.
- There are three possible forms which the term $e^{\pm \left( \omega_n \sqrt{\zeta^2-1} \right)t}$ can take:
- If $\zeta > 1$, the terms $e^{\pm \left( \omega_n \sqrt{\zeta^2-1} \right)t}$ are either growing or decaying exponentials of the form discussed in section 6.2 (if $\zeta > 1$ $e^{(\omega_n \sqrt{\zeta^2-1})t}$ grows exponentially with time and $e^{-(\omega_n \sqrt{\zeta^2-1})t}$ decays exponentially with time).
- If $\zeta=1$, the terms $e^{\pm (\omega_n \sqrt{\zeta^2-1})t}$ are constant and equal to one ($e^{\pm (0)t}=1$).
- If $\zeta<1$, the terms $e^{\pm (\omega_n \sqrt{\zeta^2-1})t}$ are complex exponentials. (The term $\sqrt{\zeta^2-1} = j \sqrt{1-\zeta^2}$, where $j=\sqrt{-1}$. Thus, the term $e^{\pm (\omega_n \sqrt{\zeta^2-1})t} = e^{\pm (j \omega_n \sqrt{1-\zeta^2})t}$ and we have an exponential raised to an imaginary power.
Before examining the above results in more detail and performing some physical, circuit-related examples, we present some material in section 8.3 relative to complex exponentials and sinusoidal signals. This material will provide us a context within which we can place our solution of equation (8.18). Section 8.3 is optional for readers who are comfortable with complex exponential and sinusoidal signals.
Section Summary
- The form of the natural response of a general second order system is:
$$y_h(t) = e^{-\zeta \omega_nt} \left[ K_1e^{(\omega_n \sqrt{\zeta^2-1})t} + K_2e^{-(\omega_n \sqrt{\zeta^2-1})t} \right]$$
Where $K_1$ and $K_2$ are constants which depend upon the system initial conditions.
- The form of the $e^{\pm (\omega_n \sqrt{\zeta^2-1})t}$ terms in the system response depends strongly upon the damping ratio. If $\zeta > 1$, these terms become growing or decaying exponentials. If $\zeta<1$, these terms are complex exponentials, and the solution will have sinusoidal components. The relationship between complex exponentials is presented in more depth in section 8.3. If $\zeta=1$, the $e^{\pm (\omega_n \sqrt{\zeta^2-1})t}$ are simply one.
- The $e^{-\zeta \omega_nt}$ term in the natural response causes the overall solution to decay as time increases. Thus, the natural response goes to zero as $t \rightarrow \infty$.
8.3: Sinusoidal Signals and Complex Exponentials
Sinusoidal signals and complex exponentials are extremely important to any engineer who is concerned with determining the dynamic response of a system. Electrical circuits, in particular, are often characterized by their response to sinusoidal inputs.
This chapter provides some background relative to these signals.
Sinusoidal Signals
Sinusoidal signals are represented in terms of sine and/or cosine functions. In general, we will represent sinusoids as cosine functions. Our general expression for a sinusoidal signal is:
$$v(t) = V_p \cos (\omega t + \theta) (Eq. 8.19)$$
Where $V_P$ is the zero-to-peak amplitude of the sinusoid, $\omega$ is the radian frequency of the sinusoid (we will always use radians/second as the units of $\omega$) and $\theta$ is the phase angle of the sinusoid (in units of either radians or degrees are used for phase angle – recall that $2\pi$ radians = 360°). A representative plot of a sinusoidal signal is provided in Figure 8.5. In Figure 8.5, the frequency of the sinusoid is indicated as a period of the signal (the period is defined as the shortest time interval at which the signal repeats itself). The radian frequency of a sinusoid is related to the period by:
$$\omega = \frac{2\pi}{T} (Eq. 8.20)$$

Note:
Complex exponential signals have both real and imaginary parts; when we introduce complex exponentials later in this chapter, we will see that the cosine function is the real part of a complex exponential signal. Complex exponentials make dynamic systems analysis relatively simple – thus, we often analyze a signals response in terms of complex exponentials. Since any measurable quantity is real-valued, taking the real part of the analytical result based on complex exponentials will result in a cosine function. Thus, cosines become a natural way to express signals which vary sinusoidally.
The frequency of a sinusoidal signal is alternately expressed in units of Hertz (abbreviated Hz). A Hertz is the number of cycles which the sinusoid goes through in one second. Thus, Hertz correspond to cycles/second. The frequency of a signal in Hertz is related to the period of the signal by:
$$f = \frac{1}{T} (Eq. 8.21)$$
Radian frequencies relate to frequencies in Hertz by:
$$f = \frac{2\pi}{\omega} \Leftrightarrow \omega = 2\pi f (Eq. 8.22)$$
Although frequencies of signals are often expressed in Hertz, it is not a unit which lends itself to calculations. Thus, all our calculations will be performed in radian frequency – if given a frequency in Hertz, it should be converted to radians/second before any calculations are performed based on this frequency.
Complex Exponentials
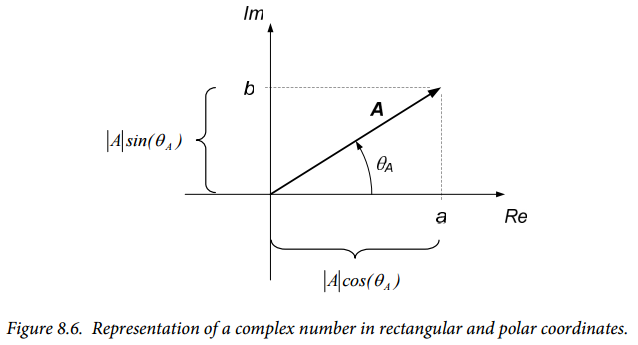
In our presentation of complex exponentials, we first provide a brief review of complex numbers. A complex number contains both real and imaginary parts. Thus, we may write a complex number $A$ as:
$$A=a+jb (Eq. 8.23)$$
Where:
$$j= \sqrt{-1} (Eq. 8.24)$$
The complex number $A$ can be represented on orthogonal axes representing the real and imaginary part of the number, as shown in Figure 8.6. (In Figure 8.6, we have taken the liberty of representing $A$ as a vector, although it is really just a number.) We can also represent the complex number in polar coordinates, also shown in Figure 8.6. The polar coordinates consist of a magnitude $|A|$ and phase angle $\theta A$, defined as:
$$|A| = \sqrt{a^2+b^2} (Eq. 8.25)$$
$$\theta_A = \tan^{-1} \left( \frac{b}{a} \right) (Eq. 8.26)$$
Notice that the phase angle is defined counterclockwise from the positive real axis. Conversely, we can determine the rectangular coordinates from the polar coordinates from:
$$a=Re \{ A \} = |A| \cos(\theta_A) (8.27)$$
$$b=Im \{ A \} = |A| \sin(\theta_A) (8.28)$$
Where the notation $Re \{ A \}$ and $Im \{ A \}$ denote the real part of $A$ and the imaginary part of $A$, respectively.
The polar coordinates of a complex number $A$ are often represented in the form:
$$A= |A| \angle \theta_A (Eq. 8.29)$$
An alternate method of representing complex numbers in polar coordinates employs complex exponential notation. Without proof, we claim that:
$$e^{j \theta} = 1 \angle \theta (Eq. 8.30)$$
Thus, $e^{j \theta}$ is a complex number with magnitude 1 and phase angle $\theta$. From Figure 8.6, it is easy to see that this definition of the complex exponential agrees with Euler's equation:
$$e^{\pm j \theta} = \cos \theta \pm j \sin \theta (Eq. 8.31)$$
With the definition of equation (8.30), we can define any arbitrary complex number in terms of complex exponentials. For example, our previous complex number $A$ can be represented as:
$$A=|A| e^{j \theta_A} (Eq. 8.32)$$
We can generalize our definition of the complex exponential to time-varying signals. If we define a time varying signal $e^{j \omega t}$ , we can use equation (8.31) to write:
$$e^{\pm j \omega t} = \cos \omega t \pm j \sin \omega t (Eq. 8.33)$$
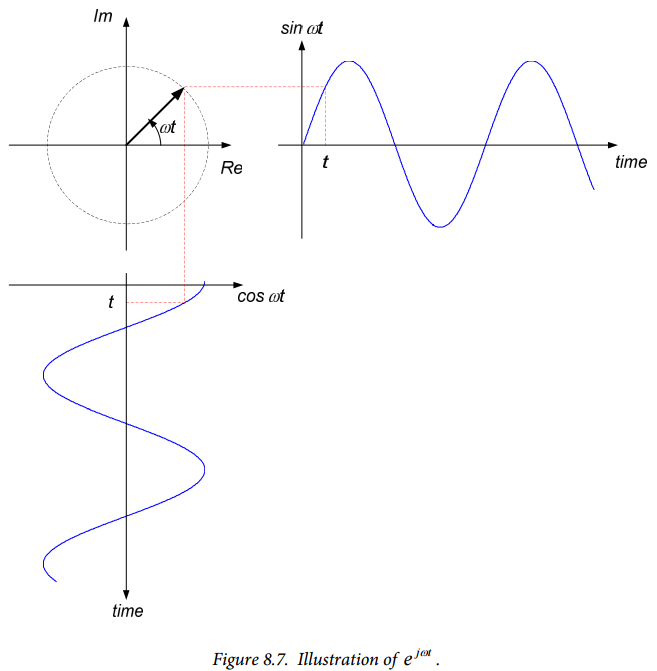
The signal $e^{j \omega t}$ can be visualized as a unit vector rotating around the origin in the complex plane; the tip of the vector scribes a unit circle with its center at the origin of the complex plane. This is illustrated in Figure 8.7. The vector rotates at a rate defined by the quantity $\omega$ – the vector makes one complete revolution every $\frac{2\pi}{\omega}$ seconds.
The projection of this rotating vector on the real axis traces out the signal $\cos \omega t$ , as shown in Figure 8.7, while the projection of the rotating vector on the imaginary axis traces out the signal $\sin \omega t$, also shown in Figure 8.7.
Thus, we interpret the complex exponential function $e^{j\omega t}$ as an alternate “type” of sinusoidal signal. The real part of this function is $\cos \omega t$ while the imaginary part of this function is $\sin \omega t$.
Section Summary
- We will represent sinusoidal signal in terms of cosine functions. The general form of our sinusoidal signals is: $v(t)=V_P \cos(\omega t + \theta)$.
- Sinusoidal signals can also be represented as complex exponentials. The relationship is an extension of Euler’s equation, and is:
$$e^{\pm j \omega t} = \cos \omega t \pm j \sin \omega t$$
- By extension, cosine signals can be represented in terms of complex exponentials as:
$$\cos(\omega t) = \frac{e^{j \omega t} + e^{-j \omega t}}{2}$$
- The above general sinusoidal signal can be expressed as the real part of a complex exponential:
$$V_P \cos (\omega t + \theta) = Re \{ V_P e^{j(\omega t + \theta)} \}$$
Exercises
- A complex valued signal $v(t)$ is given by $v(t)=e^{j(\pi t - 30^{\deg})}$. What is the real part of the signal?
- Represent the signal $v(t) = \cos (300t)$ in terms of complex exponentials.
- Represent the complex number $3-j3$ in polar coordinates.
- Represent the complex number $e^{j \pi}$ in rectangular coordinates.
- Represent the complex number $e^{\frac{-j \pi}{2}}$ in rectangular coordinates.
8.4: Second Order System Natural Response - Part 2
In section 8.2, we developed the form of the solution of the differential equation governing the natural response of second order systems. The form of the solution contained so-called complex exponentials; the background material relative to these signals was provided in section 8.3. We are thus now in a position to re-examine and interpret the solution presented in section 8.2
In section 8.2, we noted that the form of the natural response of a second order system was strongly dependent upon the damping ratio, $\zeta$. If the damping ratio was greater than one, all terms in the response decay exponentially, but if the damping ratio was between zero and one some terms in the response became complex exponentials – in section 8.3, we saw that this corresponded to an oscillating signal. Thus, depending upon the value of damping ratio, the response could decay exponentially or oscillate. In this chapter, we will quantify and formalize these results. This section concludes with an extended example of a second order system natural response.
In section 8.1, the differential equation governing the natural response of a second order system was written as:
$$\frac{d^2y_h(t)}{dt^2} + 2 \zeta \omega_n \frac{dy_h(t)}{dt} + \omega_{n}^{2} y_h (t) = 0 (Eq. 8.34)$$
Where $y(t)$ is any system parameter of interest, $\omega_n$ is the undamped natural frequency and $\zeta$ is the damping ratio. The initial conditions are the value of the function $y(t)$ at $t = 0$ and the derivative of the function $y(t)$ at $t = 0$:
$$y(t=0)=y_0$$ $$\frac{dy(t)}{dt} |_{t=0} = y^{'}_0 \\ (Eq. 8.35)$$
In section 8.2, we wrote the solution to equation (8.34) in the form:
$$y_h(t) = e^{-\zeta \omega_n t} \left[ K_1e^{(\omega_n \sqrt{\zeta^2-1})t} + K_2e^{-(\omega_n \sqrt{\zeta^2-1})t} \right] (Eq. 8.36)$$
Where $K_1$ and $K_2$ are unknown coefficients which can be determined by application of the initial conditions provided in equation (8.35). The form of the solution of equation (8.36) will fall into one of three categories, depending on the value of damping ratio. The three possible cases are:
- If $\zeta > 1$, all terms in the solution will be either growing or decaying exponentials and the solution will decay exponentially with time. If the damping ratio is large, this decay rate can be very slow. A system with $\zeta > 1$ is said to be overdamped.
- If $\zeta < 1$, the terms $e^{\pm (\omega_n \sqrt{\zeta^2-1})t}$ are complex exponentials. Thus, have terms in our solution which are exponentials raised to an imaginary power and the solution can oscillate. A system with $\zeta < 1$ is said to be underdamped.
- $\zeta=1$; the form of the solution in this case is approximately that of case 1 above, in that the solution will decay exponentially. However, in this case, the response decay rate will be faster than the response of any overdamped system with the same natural frequency. Systems with $\zeta=1$ are said to be critically damped.
Details of the responses for each of the above three cases are provided in the subsections below.
1. Overdamped System
For an overdamped system, $\zeta>1$, and equation (8.36) becomes as shown in equation (8.37).
$$y_h(t)=e^{-\zeta \omega_nt} \left[ \frac{\dot{y}_0 + (\zeta + \sqrt{\zeta^2-1}) \omega_ny_0}{2 \omega_n \sqrt{\zeta^2-1}} e^{\omega_nt \sqrt{\zeta^2-1}} + \frac{\dot{y}_0 - (\zeta- \sqrt{\zeta^2-1})\omega_ny_0}{2\omega_n \sqrt{\zeta^2-1}} e^{-\omega_n t \sqrt{\zeta^2-1}} \right] (Eq. 8.37)$$
In equation (8.37), the $e^{-\zeta \omega_n t}$ term is a decaying exponential with time constant $\frac{1}{\zeta \omega_n}$. The $e^{\omega_n t \sqrt{\zeta^2-1}}$ is a growing exponential with time constant $\frac{1}{\omega_n \sqrt{\zeta^2-1}}$. Thus, the overall system response is a sum of two decaying exponential signals, one which is proportional to $e^{-\zeta \omega_n t} \cdot e^{\omega_n t \sqrt{\zeta^2-1}}$ and the other which is proportional to $e^{-\zeta \omega_n t} \cdot e^{-\omega_n t \sqrt{\zeta^2-1}}$.
The term $e^{-\zeta \omega_n t} \cdot e^{\omega_n t \sqrt{\zeta^2-1}}$ is the product of two exponentials: one which grows with time, and the other which decays with time. The decaying exponential time constant, $\frac{1}{\zeta \omega_n}$, is smaller than the growing exponential time constant, $\frac{1}{\omega_n \sqrt{\zeta^2-1}}$. Thus, the product of the two will decay with time, though the decay rate may be very slow. (Note that in the limit as $\zeta \rightarrow \infty$, $\frac{1}{\zeta \omega_n} \approx \frac{1}{\omega_n \sqrt{\zeta^2-1}}$, the two time constants are nearly identical, and this term becomes constant with time.)
The term $e^{\zeta \omega_n t} \cdot e^{-\omega_n t \sqrt{\zeta^2-1}}$ is the product of two decaying exponentials; this term will, in general, decay quickly relative to the $e^{\zeta \omega_n t} \cdot e^{-\omega_n t \sqrt{\zeta^2-1}}$ term.
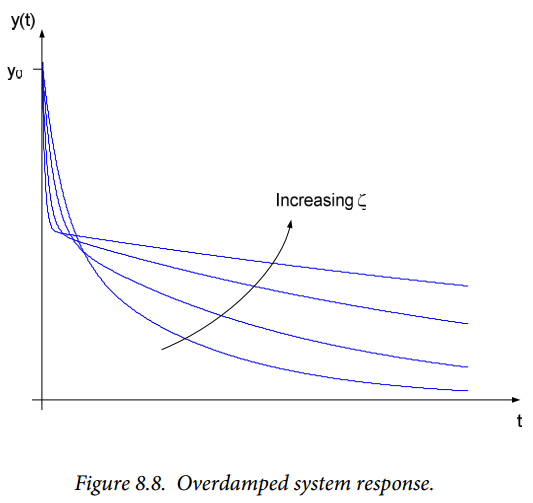
An example of the response of an overdamped system is shown in Figure 8.8, for various values of damping ratio. The two system time constants are readily observable in this example. Note that as the damping ratio increases, the overall time required for the system response to decay to zero increases. The response of overdamped systems cannot oscillate, however, the response can change sign once (e.g. the function is allowed one zero-crossing).
2. Underdamped System
For an underdamped system, $\zeta <1$, and equation (8.36) becomes as shown in equation (8.38).
$$y_h(t)=e^{-\zeta \omega_n t} \left[ \frac{\dot{y}_0 + \zeta \omega_n y_0}{\omega_n \sqrt{1-\zeta^2}} \sin \left( \omega_n t \sqrt{1-\zeta^2} \right) + y_0 \cos \left( \omega_n t \sqrt{1-\zeta^2} \right) \right] (Eq. 8.38)$$
The solution is a decaying sinusoid. The decay rate is set by the term $e^{-\zeta \omega_n t}$, while the oscillation frequency of the sinusoid is $\omega_n \sqrt{1-\zeta^2}$. The oscillation frequency seen in the natural response is thus not identically the natural frequency of the system; it is also influenced by the damping ratio. This leads to the definition of the damped natural frequency:
$$\omega_d = \omega_n \sqrt{1-\zeta^2} (Eq. 8.39)$$
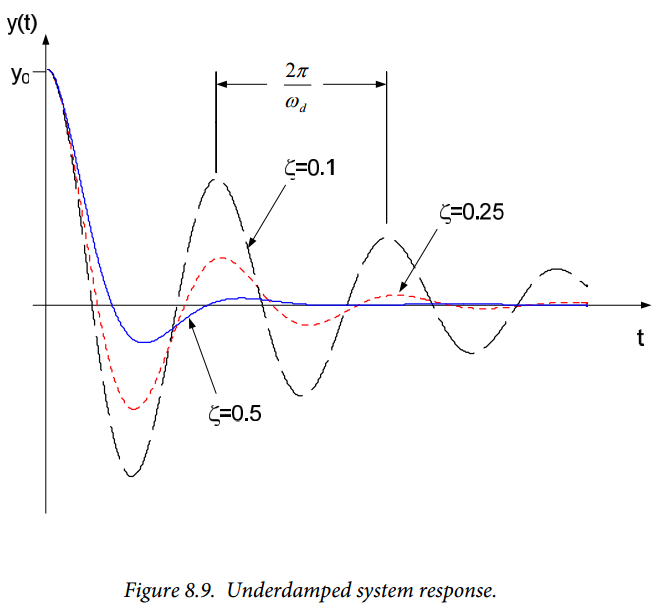
Oscillations seen in the system response will have radian frequency $\omega_d$; thus, the period of the oscillations is $\frac{2 \pi}{\omega_d}$.
Example responses for underdamped systems are shown in Figure 8.9; the responses shown are all for the same natural frequency and initial conditions – only the damping ratio varies. Note that smaller damping ratios result in slower decay rates for the response, oscillations persist for longer and are more pronounced for smaller damping ratios.
3. Critically Damped System
For a critically damped system, $\zeta=1$, and equation (8.36) becomes as shown in equation (8.40).
$$y_h(t) = e^{-\zeta \omega_n t} \left[ y_0 + (\dot{y}_0 + \omega_n y_0 t) \right] (Eq. 8.40)$$
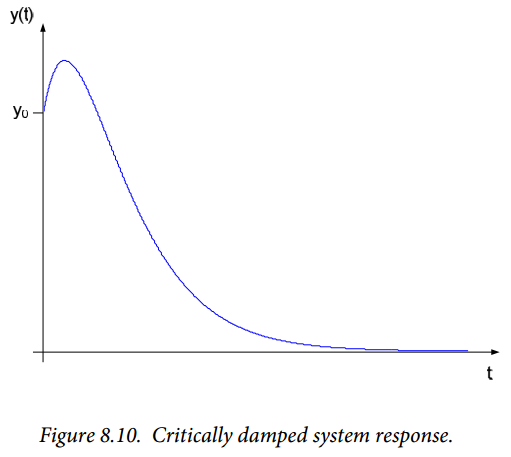
The critically damped system response does not oscillate although, as with the overdamped case, one zero crossing of the function is allowed. The importance of the critically damped system response is that, for a particular natural frequency, it has the shortest decay time without oscillation of any system. An example response of a critically damped system is shown in Figure 8.10.
Example 8.3
For the circuit shown below:
- Write the differential equation for $v_C(t)$.
- If $L = 1H$, $R = 200\Omega$, and $C = 1x10^{-6}F$, find the undamped natural frequency, the damping ratio, and the damped natural frequency.
- For the conditions in part (2), is the system underdamped, overdamped, or critically damped?
- For the values of L and C in part (2), determine the value of R that makes the system critically damped.
- If $v_C(0) = 1V$ and $i_L(0) = 0.01A$, what are the appropriate initial conditions to solve the differential equation determined in part (1)?
a.) As usual, we define the voltage across the capacitor and the current through the inductor as our variables and write KVL and KCL in terms of these variables. The figure below shows these variables, along with the associated currents through capacitors and voltages across inductors.
KCL at the indicated node results in:
$$i_L(t) + C \frac{dv_C(t)}{dt}=0 (Eq. 8.41)$$
KVL around the indicated loop provides:
$$L\frac{di_L(t)}{dt} + 2Ri_L(t)=v_C(t) (Eq. 8.42)$$
The above two equations can be combined to obtain an equation for $v_C(t)$. To do this, we use the first equation to obtain:
$$i_L(t)=-C \frac{dv_C(t)}{dt} (Eq. 8.43)$$
Differentiating equation (8.43) provides:
$$\frac{di_L(t)}{dt} = -C\frac{d^2v_C(t)}{dt^2} (Eq. 8.44)$$
Substituting equations (8.43) and (8.44) into equation (8.42) results in:
$$-LC \frac{d^2v_C(t)}{dt^2} -2RC \frac{dv_C(t)}{dt} = v_C(t)$$
Dividing the above by LC and grouping terms gives our final result:
$$\frac{d^2v_C(t)}{dt^2} + \frac{2R}{L} \frac{dv_C(t)}{dt} + \frac{1}{LC} v_C(t) = 0 (Eq. 8.45)$$
b.) Equation (5) is of the form:
$$\frac{d^2y(t)}{dt^2} + 2 \zeta \omega_n \frac{dy(t)}{dt} + \omega_{n}^{2} y(t) = 0 (Eq. 8.46)$$
Equating coefficients in equations (8.45) and (8.46) and substituting $L = 1H$, $R = 200\Omega$, and $C = 1x10^{-6}F$ results in:
$$2 \zeta \omega_n = \frac{2R}{L} = 400 (Eq. 8.47)$$
$$\omega_{n}^{2} = \frac{1}{LC} = 1x10^6 (Eq. 8.38)$$
Solving equation (8) for the natural frequency results in $\omega_n = 1000$ rad/sec. Substituting this result into equation (8.47) and solving for the damping ratio gives $\zeta = 0.2$. The damped natural frequency is:
$$\omega_d = \omega_n \sqrt{1-\zeta^2} = 979.8 rad/sec$$
c.) The damping ratio determined in part (b) is $\zeta = 0.2$; since this is less than one, the system is underdamped.
d.) In order for the system to be critically damped, the damping ratio $\zeta = 1$. From equation (8.47) with $\zeta = 1$, we obtain:
$$2 \zeta \omega_n = \frac{1R}{L} \Rightarrow 2(1)(1000) = \frac{2R}{1H} \Rightarrow R = 1000 \Omega$$
e.) Initial conditions on $v_C(t)$ are $v_C(0)$ and $\frac{dv_C(t)}{dt} |_{t=0}$ We are given $v_C(-)=1V$ in the problem statement, but we need to determine $\frac{dv_C(t)}{dt} |_{t=0}$; the current through the inductor, $i_L(0)$ can be used to determine this. The current through the inductor is related to the capacitor voltage via equation (8.43) above:
$$i_L(t)=-C \frac{dv_C(t)}{dt}$$
so at time $t=0$,
$$i_L(0)=-(1x10^{-6}F) \frac{dv_C(t)}{dt} |_{t=0}=0.01A$$
Solving for $\frac{dv_C(t)}{dt} |_{t=0}$,
$$\frac{dv_C(t)}{dt}|_{t=0} = \frac{1}{C}i_L(0) = -\frac{0.01A}{1x10^{-6}F} = -10,000 V/sec$$
We conclude this example with plots of the system response for underdamped, critically damped, and overdamped conditions.
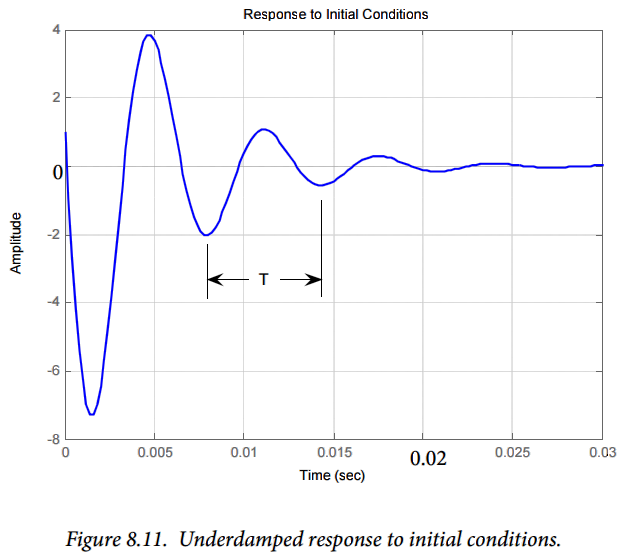
Figure 8.11 shows the response of the circuit described by the differential equation determined in part (a) above, for the circuit parameters provided in part (b), to the initial conditions of part (e). Thus, the governing differential equation is
$$\frac{d^2v_C(t)}{dt^2} + \frac{2R}{L} \frac{dv_C(t)}{dt} + \frac{1}{LC} v_C(t)=0$$
With $L=1H$, $R=200 \Omega$, and $C=1x10^{-6}F$, the differential equation becomes:
$$\frac{d^2v_C(t)}{dt^2} + 400 \frac{dv_C(t)}{dt} + 1x10^6 v_C(t)=0$$
The initial conditions are, from part (e):
$$v_C(0)=1V$$
$$\frac{dv_C(t)}{dt}|_{t=0} = -10,000 V/sec$$
Using MATLAB to evaluate the differential equation results in Figure 8.11. Figure 8.11 agrees with our expectations based on the calculations of part (b). In part (b), we determined that the damping ratio $\zeta = 0.2$, so that the system is underdamped – Figure 8.11 exhibits the oscillations (multiple zero axis crossings) that we would expect from an underdamped system. Likewise, we determined in part (b) that the damped natural frequency of the system is approximately 980 rad/sec. The period of the oscillations we would expect to see in the response is therefore:
$$T=\frac{2 \pi}{\omega_d} = 0.0064 seconds$$
This value is consistent with the period of the oscillations seen in Figure 8.11.
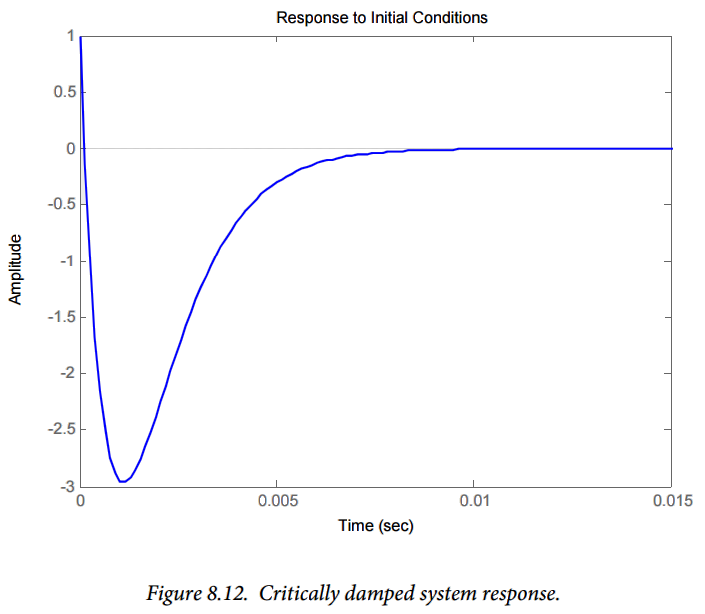
In part (d) above, we determined that the value of R resulting in a critically damped system is $R = 1000\Omega$. Re- evaluating the above governing differential equation with this value for R results in
$$\frac{d^2v_C(t)}{dt^2} + 2000 \frac{dv_C(t)}{dt} + 1x10^6 v_C(t)=0$$
the initial conditions are as in the above example:
$$v_C(0)=1V$$
$$\frac{dv_C(t)(t)}{dt} |_{t=0} = -10,000 V/sec$$
The resulting response is shown in Figure 8.12. This plot also matches our expectations, though we have fewer quantitative results against which to compare it. The response does not oscillate (the response does have one and only one zero crossing, which is allowable for a critically damped or overdamped system. The response also appears to be composed of exponential signals, which is consistent with our expectations.
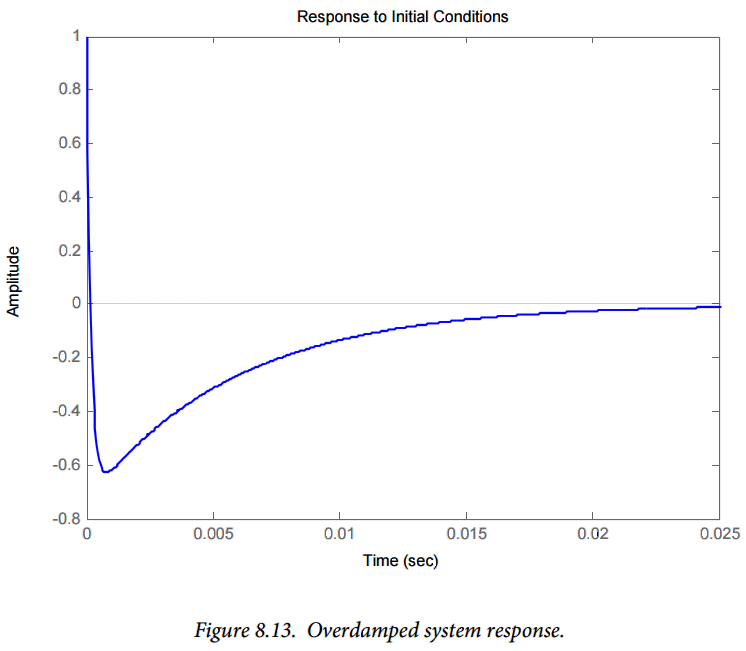
In order to obtain a better understanding of critically damped vs. overdamped systems, we increase R to $3000\Omega$. The resulting damping ratio is $\zeta = 3$; increasing R above the critically damped value will result in an overdamped system since the damping ratio is proportional to R. We will expect the response shape to be somewhat like that shown in Figure 8.12 (it will still be composed of decaying exponential functions) but the overdamped system should decay more slowly. This overdamped system response is shown in Figure 8.13. This response agrees with our qualitative expectations – the response does not oscillate, and the decay time is longer than that shown in Figure 8.12.
Section Summary
- It is common to categorize second order systems by their damping ratio. This also characterizes the shape of their natural response. The three categories are:
- If $\zeta > 1$, the system is said to be overdamped. For this case, the response will decay exponentially with time with no oscillations. If the damping ratio is large, this decay rate can be very slow.
- If $\zeta < 1$, the system is said to be underdamped. In this case, the natural response can oscillate. Increasing the damping ratio tends to reduce the amplitude of the oscillations, and cause the oscillations to die out more quickly.
- $\zeta = 1$, the solution is said to be critically damped. In this case, the response will not oscillate, and the decay rate of the response will be faster than the response of any overdamped system with the same natural frequency.
For an underdamped system, the oscillations observed in the response have a radian frequency $\omega_d$ defined as:
$$\omega_d= \omega_n \sqrt{1-\zeta^2}$$
$\omega_d$ is called the damped natural frequency of the system. The period of the oscillations in the natural frequency (the time between successive peaks) is $\frac{2 \pi}{\omega_d}$.
Exercises
1. The differential equation governing a circuit with output $y(t)$ is given by:
$$\frac{d^2y(t)}{dt^2} + 6\frac{dy(t)}{dt} + 144y(t) = 0$$
What are the damping ratio and natural frequency of the circuit? Is the circuit under-, over-, or critically damped?
2. The differential equation governing a circuit’s natural response is:
$$\frac{d^2y(t)}{dt^2} + 32\frac{dy(t)}{dt} + 64y(t) = 0$$
Where $y(t)$ is the circuit response. What are:
- The circuit’s natural frequency,
- The circuit’s damping ratio, and
- The two time constants governing the circuit
3. The differential equation governing a circuit’s natural response is:
$$\frac{d^2y(t)}{dt^2} + 8 \frac{dy(t)}{dt} + 64y(t)=0$$
Where $y(t)$ is the circuit response. What are:
- The circuit’s natural frequency,
- The circuit’s damping ratio, and
- The circuit's damped natural frequency?
8.5: Second Order System Step Response
In this section, we address the case in which the input to a second order system consists of the sudden application of a constant voltage or current to the circuit; this type of input can be modeled as a step function. The response of a system to this type of input is called the step response of the system.
The material presented in this section will emphasize the development of qualitative relationship between the damping ratio and natural frequency of a system and the system’s time-domain response. We will also see that we can quantitatively relate several specific response parameters to the system’s damping ratio and natural frequency. This approach allows us to infer a great deal about the expected system response directly from the damping ratio and natural frequency of the system, without explicitly solving the differential equation governing the system. This approach is also useful in system design, since we can readily determine the damping ratio and natural frequency necessary to provide the desired response shape. Since the damping ratio and natural frequency are typically functions of resistances, capacitances, and inductances, we can readily design a system to produce the desired response.
In section 8.1, we wrote a general differential equation governing a second order system as:
$$\frac{d^2y(t)}{dt^2} + 2 \zeta \omega_n \frac{dy(t)}{dt} + \omega_{n}^{2}y(t)=f(t) (Eq. 8.49)$$
Where $y(t)$ is any system parameter of interest (for example, a voltage or current in an electrical circuit), $\omega_n$ and $\zeta$ are the undamped natural frequency and the damping ratio of the system, respectively, and $f(t)$ is a forcing function applied to the system.
In this chapter section, we restrict our attention to the specific case in which $f(t)$ is a step function. Thus, the forcing function to the system can be written as:
$$f(t)= Au_0(t)= \begin{cases} 0, t < 0 \\ A, t > 0 \\ \end{cases} (Eq. 8.50)$$
Thus, the differential equation governing the system becomes:
$$\frac{d^2y(t)}{dt^2} + 2 \zeta \omega_n \frac{dy(t)}{dt} + \omega_{n}^{2} y(t) = Au_0(t) (Eq. 8.51)$$
In addition to the above restriction on the forcing function, we will assume that the initial conditions are all zero (we sometimes say that the system is initially relaxed). Thus, for the second-order system above, our initial conditions will be:
$$y(t=0)=0 \\ \frac{dy(t)}{dt} |_{t=0} =0 \\ (Eq. 8.52)$$
Solving equation (8.51) with the initial conditions provided in equations (8.52) results in the step response of the system.
As in our discussion of forced first order system responses in section 8.1, we write the overall solution of the differential equation of equation (8.51) as the sum of a particular solution and a homogeneous solution. Thus:
$$y(t)=y_h(t) + y_p(t)$$
The homogeneous solution of second order differential equations has been discussed in sections 8.1 and 8.4 and will not be repeated here. The particular solution of the differential equation (8.51) can be obtained by examining the solution to the equation after the homogeneous solution has died out. Letting $t \rightarrow \infty$ in equation (8.51) and noting that the forcing function is a constant as $t \rightarrow \infty$ allows us to set $\frac{d^2y(t \rightarrow \infty)}{dt^2} = \frac{dy(t \rightarrow \infty)}{dt} = 0$ and thus,
$$\omega_{n}^{2} y_P(t) = A \Rightarrow y_P(t) = \frac{A}{\omega_{n}^{2}} (Eq. 8.53)$$
Combining the particular and homogeneous solutions, assuming the system is underdamped $(\zeta < 1)$, and employing the initial conditions results in our final expression for the step response of an underdamped second order system:
$$y(t) = \frac{A}{\omega_{n}^{2}} \{ 1-e^{- \zeta \omega_n t} [ \cos (\omega_d t) + \frac{\zeta}{\sqrt{1-\zeta^2}} \sin (\omega_d t) ] \} (Eq. 8.54)$$
Where $\omega_d = \omega_n \sqrt{1-\zeta^2}$ is the damped natural frequency of the system, previously defined in chapter 8.4.
It is common to interpret an underdamped second order system’s response in terms of the damping ratio and the natural frequency, rather than direct evaluation of equation (8.54). Figure 8.14 shows a typical step response for an underdamped second order system. The system response overshoots to a maximum value $y_p$ and has steady- state response $y_{ss}$. The maximum overshoot is generally normalized by the steady-state response and is presented in terms of a variable $M_P$ defined as:
$$M_P = \frac{y_P-y_{ss}}{y_{ss}} (Eq. 8.55)$$
$M_P$ is often presented as a percent, obtained by multiplying equation (8.55) by 100. Other parameters of interest in characterizing the step response are the period of any oscillations in the response (T in Figure 8.14) and the rise time, $t_r$. The rise time is defined as the time required for the system response to go from 10% to 90% of the steady state response. The rise time is often used as an indication of how quickly a second order system responds.
The time domain parameters $M_P$, $t_r$, and $T$ are readily related to the parameters $\xi$, $\omega_n$, and $\omega_d$. We provide the following relations here, without proof:
$$M_P = e^{\frac{-\pi \xi}{\sqrt{1-\xi^2}}} (Eq. 8.56)$$
$$t_r \approx \frac{1.8}{\omega_n} (Eq. 8.57)$$
Note: for small damping ratios, ($\xi < 0.6$), equation (8.56) is often approximated as:
$$M_P \approx - \frac{\xi}{0.06} (Eq. 8.59)$$
Section Summary
- Typical parameters used to characterize the step response of an underdamped system are the rise time, the maximum overshoot, and the frequency of the oscillations in the response. These parameters are defined as follows:
- The rise time, $t_r$, is the time required for the response to go from 10% to 90% of its steady-state response
- The maximum overshoot provides the maximum value achieved by the response. The maximum overshoot is a normalized value, defined as:
$$M_P = \frac{y_p-y_{ss}}{y_{ss}}$$
Where $y_p$ is the peak (or maximum) value of the response and $y_{ss}$ is the steady state system response. $M_P$ is often expressed as a percent, by multiplying the above quantity by 100.
- The radian frequency of the oscillations in the step response is given by the damped natural frequency:
$$\omega_d = \omega_n \sqrt{1-\zeta^2}$$
The period of the oscillations in the response is then given by:
$$T= \frac{2 \pi}{\omega_d}$$
- The rise time and maximum overshoot can be related to the damping ratio and natural frequency of the system. The appropriate relations are provided below:
- $t_r \approx \frac{1.8}{\omega_n}$
- $M_P=e^{\frac{- \pi \xi}{\sqrt{1-\xi^2}}}$ or $M_P - \frac{\xi}{0.6}$ (for small damping ratios, $\xi < 0.6$)
The period of the oscillations can be used to cross-check the above results, since it depends upon both the damping ratio and natural frequency.
Exercises
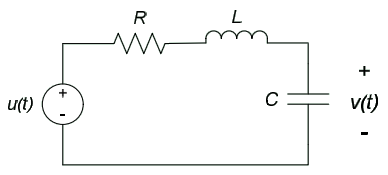
- The differential equation governing the circuit shown below is:
$$\frac{d^2v(t)}{dt^2} + 12 \frac{dv(t)}{dt} + 400v(t) = 400u(t)$$
If $u(t)=2u_0(t)$, what are:
- The circuit’s natural frequency,
- The circuit’s damping ratio,
- The percent overshoot ($M_P$), the rise time ($t_r$), and the steady-state response of the capacitor voltage
- What is the maximum value seen by the capacitor voltage?