Real Analog: Chapter 12
- Chapter 12 Materials
-
- Lecture Material:
- Lecture 31 PowerPoint Slides: Sinusoidal steady-state power, instantaneous & average power, reactive power, complex power, power factor
- Lecture 32 PowerPoint Slides: Review: AC power analysis (average & complex power, power triangles, RMS values, power factor), power factor correction
- Chapter 12 Video:
- Lab 12 Video 1: AC Power & Power Factor: An example of the role of power factor in the transmission of AC power. Power factor correction is used to improve the efficiency of power transmission.
-
- Exercise Solutions: Chapter 12 exercise solutions
- Homework: Chapter 12 homework problems
12. Introduction and Chapter Objectives
In this chapter we will address the issue of power transmission via sinusoidal (or AC) signals. This topic is extremely important, since the vast majority of power transmission in the world is performed using AC voltages and currents.
For the most part, the topic of AC power transmission focuses on the average power delivered to a load over time. In general, it is not productive to focus on the power transmission at a particular time since, if the load contains energy storage elements (such as capacitors and inductors), it is possible that at times the load will absorb power and at other times the load will release power. This characteristic leads to the concepts of average power and reactive power – average power is typically the power that is converted by the load to useful work, while reactive power is the power that is simply exchanged by energy storage elements. Power companies cannot really charge customers for power which is not absorbed by the load, so one primary goal in AC power transmission is to reduce the reactive power that is sent to the load.
In this chapter we introduce the basic topics relative to calculation of AC power. In section 12.1, we introduce the basic concepts associated with AC power, including the notion that a load containing energy storage elements may alternately absorb and release power. This discussion will lead to the concepts of average power and reactive power, which are discussed in section 12.2. Power calculations are often presented in terms of RMS values; these are introduced in section12.3. The relative roles of average and reactive power are often characterized by the apparent power and the power factor, which are presented in section 12.4. In section 12.5, we will use complex numbers to simultaneously quantify the average power, the reactive power, the apparent power, and the power factor. Finally, in section 12.6, we examine approaches to reduce the reactive power which is exchanged between the power company and the user. This technique is called power factor correction.
After Completing this Chapter, You Should be Able to:
- Define instantaneous power, average power, and reactive power
- Define real power, reactive power, and complex power
- Define RMS signal values and calculate the RMS value of a given sinusoidal signal
- State, from memory, the definition of power factor and calculate the power factor from a given combination of voltage and current sinusoids
- Draw a power triangle
- Correct the power factor of an inductive load to a desired value
12.1: Instantaneous Power
We will begin our study of steady-state sinusoidal power by examining the power delivered by a sinusoidal signal as a function of time. We will see that, since all the signals involved are sinusoidal, the delivered power varies sinusoidally with time. This time-varying power is called instantaneous power, since it describes the power delivered to the load at every instant in time. The instantaneous power will not, in general, be directly useful to us in later sections but it does provide the basis for understanding the concepts presented throughout this chapter.
In chapter 1, we saw that power is the product of voltage and current, so that power as a function of time is:
$$p(t)=v(t) \cdot i(t) (Eq. 12.1)$$
Power as a function of time is often called instantaneous power, since it provides the power at any instant in time. So far, this is the only type of power with which we have been concerned. If our voltages and currents are sinusoidal, as is the case for AC power, we can write $v(t)$ and $i(t)$ as:
$$v(t) = v_m \cos(\omega t + \theta_v) (Eq. 12.2)$$
And:
$$i(t) = I_m \cos(\omega t+ \theta_i) (Eq. 12.3)$$
Where, of course, $V_m$ and $\theta_v$ are the amplitude and phase angle of the voltage signal while $I_m$ and $\theta_i$ are the amplitude and phase angle of the current signal. It should be noted at this point that the voltage and current signals of equations (12.2) and (12.3) are not independent of one another. Figure 12.1 shows the overall system being analyzed – the voltage $v(t)$ and the current $i(t)$ are the voltage and current applied to some load. If the load has some impedance, $Z_L$, the voltage and current are related through this impedance. Thus, if we represent $v(t)$ and $i(t)$ in phasor form as $p(t) = v(t)$ and $i(t)=\underline{I}e^{j \omega t}$, then $\underline{V}=Z_L \cdot \underline{I}$.
Substituting equations (12.2) and (12.3) into equation (12.1) results in:
$$p(t)=V_mI_m \cos(\omega t + \theta_v) \cos(\omega t + \theta_i) (Eq. 12.4)$$
Equation (12.4) can be re-written, using some algebra and trigonometric identities, as:
$$p(t) = \frac{V_m I_m}{2} \left\{ \cos(\theta_v - \theta_i) + \cos(2 \omega t + \theta_v + \theta_i) \right\} (Eq. 12.5)$$
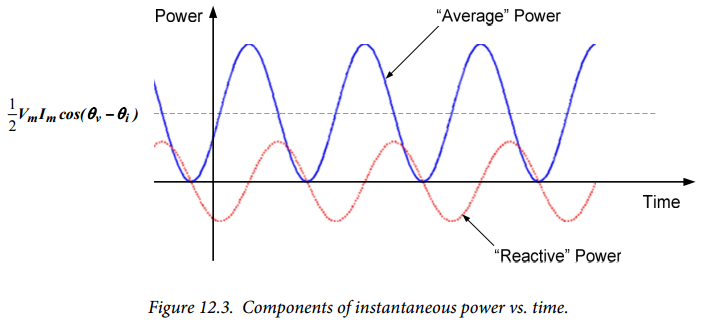
Since $V_m$, $\theta_v$, $I_m$, and $\theta_I$ are all constants, we can see that equation (12.5) is the sum of two terms: a constant value, $\frac{V_m I_m}{2} \cos(\theta_v - \theta_i)$, and a sinusoidal component, $\frac{V_m I_m}{2} \cos(2 \omega t + \theta_v + \theta_i)$. The time-domain relationship of equation (12.5) is plotted in Figure 12.2. The signal's average value is $\frac{V_m I_m}{2} \cos(\theta_v - \theta_i)$ and has a sinusoidal component with an amplitude of $\frac{V_m I_m}{2}$.
Section Summary
- The power delivered to a load by a sinusoidal (or AC) signal has two components: an average value and a sinusoidal component.
- Both the average value and the sinusoidal component are dependent upon the amplitude and phase angles of the voltage and current delivered to the load. These values are, in turn, set by the impedance of the load.
- The average power is dissipated or absorbed by the load. This power is electrical power which is converted to heat or useful work.
- The sinusoidal component of the power is due to energy storage elements in in the load; this power is exchanged (in some sense) between the load and the system supplying power. It is purely electrical energy which the load is not using to perform useful work.
Exercises
- The current and voltage delivered to a load are $i(t) = 2 \cos(100t)$ and $v(t) = 120 \cos(100t+65^{\circ})$, respectively. Calculate the average power delivered to the load and the amplitude of the sinusoidal component of the power.
12.2: Average and Reactive Power
Examination of equation (12.5) and Figure (12.2) indicates that the instantaneous power can be either positive ornegative, so the load is alternately absorbing or releasing power. The overall amount of power absorbed vs. power released is dependent primarily upon the $\cos(\theta_v - \theta_i)$ term. If the voltage and current are in phase, $\theta_v = \theta_i$, $\cos(\theta_v - \theta_i ) = 1$ and the instantaneous power is never negative. The voltage and current have the same phase if the load is purely resistive – a resistor always absorbs power. If the voltage and current are $90^{\circ}$ out of phase, as is the case for a purely capacitive or purely inductive load, $\cos(\theta_v - \theta_i) = 0$. In this case, the instantaneous power curve is a pure sinusoid with no DC offset, so on average no power is delivered to the load. This is consistent with our models of capacitors and inductors as energy storage elements, which do not dissipate any energy.
The concepts presented in the paragraph above can be mathematically presented by rearranging equation (12.5) yet again. Application of additional trigonometric identities and performing more algebra results in:
$$p(t) = \frac{V_m I_m}{2} \cos(\theta_v - \theta_i) [1+ \cos(2 \omega t)] + \frac{V_m I_m}{2} \sin(\theta_v - \theta_i) [\sin(2 \omega t)] (Eq. 12.6)$$
The two terms in equation (12.6) are plotted separately in Figure 12.3. The first term, $\frac{V_m I_m}{2} \cos(\theta_v - \theta_i) [1+ \cos(2 \omega t)]$, has an average value of $\frac{V_m I_m}{2} \cos(\theta_v - \theta_i)$, while the second term, $\frac{V_m I_m}{2} \sin(\theta_v - \theta_i) [ \sin(2 \omega t)]$, has an average value of zero. Thus, the average power delivered to a load is:
$$P=\frac{V_m I_m}{2} \cos(\theta_v - \theta_i) (Eq. 12.7)$$
The amplitude of the term $\frac{V_m I_m}{2} \sin(\theta_v - \theta_i) [ \sin(2 \omega t)]$, which provides no average power to the load, is termed the reactive power, Q:
$$Q = \frac{V_m I_m}{2} \sin(\theta_v - \theta_i) (Eq. 12.8)$$
The reactive power is a measure of the amount of power which is delivered to the load, but is not absorbed by the load – the load returns this power to the source!
Section Summary
- The average power delivered to a load is:
$$P= \frac{V_m I_m}{2} \cos(\theta_v - \theta_i)$$
Where $V_m$ and $\theta_v$ are the amplitude and phase angle of the voltage while $I_m$ and $\theta_i$ are the amplitude and phase angle of the current. The average power is often also called the real power. The average power is also the power dissipated by any resistive elements in the load. Units of average power are Watts (abbreviated W).
- The reactive power dellivered to a load is:
$$Q = \frac{V_m I_m}{2} \sin(\theta_v - \theta_i)$$
The reactive power is not actually absorbed by the load; it is stored by the energy storage elements in the load and then returned to the source. The units of reactive power are taken to be Volt-Amperes Reactive (abbreviated VAR). Note that technically watts are the same as volt-amps, but we have changed terminology to avoid any confusion between real and reactive power.
Exercises
- The current and voltage delivered to a load are $i(t) = 2 \cos(100t)$ and $v(t) = 120 \cos(100t+65^{\circ})$, respectively. Calculate the average power delivered to the load and the reactive power delivered to the load.
12.3: RMS Values
In sections 12.1 and 12.2, we introduced some basic quantities relative to delivery of power using sinusoidal signals. We saw that power dissipated by a load (essentially, any energy which is converted to non-electrical energy such as heat or work) is the average power. Reactive power results from energy which is stored by capacitors and inductors in the load and is then returned to the source without dissipation.
In this chapter, we continue our study of AC power analysis. We will introduce the concept of the root-mean- square (RMS) value of a signal as a way to represent the power of a time-varying signal. We will also introduce complex power as a way to conveniently represent both average and reactive power as a single complex number. We also introduce power factor as a way to represent the efficiency of the transfer of power to a load.
It is often desirable to compare different types of time-varying signals (for example, square waves vs. triangular waves vs. sinusoidal waves) using a very simple metric. Different types of signals are often compared by their RMS (root-mean-squared) values. The general idea behind the RMS value of a time-varying signal is that we wish to determine a constant value, which delivers the same average power to a resistive load.
The average value, $P$, of an instantaneous power $p(t)$ is defined to be:
$$P = \frac{1}{T} \int^{t_0 + r}_{t_0} p(t)dt (Eq. 12.9)$$
The power delivered to a resistive load by a constant voltage or current source is, from chapter 1.1,
$$P=R \cdot I_{eff}^{2} = \frac{V^2_{eff}}{R} (Eq. 12.10)$$
$I_{eff}$ and $V_{eff}$ are the effective (or constant) current and voltage, respectively, applied to the resistive load, $R$. It is our goal to equate equations (12.9) and (12.10) to determine the effective voltage or current values, which deliver the same average power to a resistive load as some time-varying waveform.
Assuming that a current is applied to a resistive load, the instantaneous power is $p(t) = R \cdot i^2 (t)$. Substituting this into equation (12.9) and equating to equation (12.10) results in:
$$R \cdot I_{eff}^2 = \frac{1}{T} \int\limits_{t_0}^{t_0 + T} R \cdot i^2 (t)dt (Eq. 12.11)$$
Solving this for $I_{eff}$ results in:
$$I_{eff} = I_{RMS} = \sqrt{\frac{1}{T} \int\limits_{t_0}^{t_0 + T} i^2 (t)dt} (Eq. 12.12)$$
And the effective current is the square root of the mean of the square of the time-varying current. This is also called the RMS (or root-mean-square) value, for rather obvious reasons.
A similar process can be applied to the voltage across a resistive load, so that $p(t)= \frac{v^2(t)}{R}$. Equating this expression to equation (12.9) results in:
$$V_{eff} = V_{RMS} = \sqrt{\frac{1}{T} \int\limits_{t_0}^{t_0 + T} v^2 (t)dt} (Eq. 12.13)$$
So that the definition of an RMS voltage is equivalent to the definition of an RMS current.
Equations (12.12) and (12.13) are applicable to any time-varying waveform; the waveforms of interest to us are sinusoids, with zero average values (per equations (12.10) and (12.11)). In this particular case, the RMS values can be calculated to be:
$$V_{eff} = V_{RMS} = \frac{V_m}{\sqrt{2}} (Eq. 12.14)$$
And:
$$I_{eff} = I_{RMS} = \frac{I_m}{\sqrt{2}} (Eq. 12.15)$$
Where $V_m$ and $I_m$ are the peak (or maximum) values of the voltage and current waveforms, per equations (12.10) and (12.11). Please note that equations (12.14) and (12.15) are applicable only to sinusoidal signals with zero average values.
The average and reactive powers given by equations (12.16) and (12.17) can be written in terms of the RMS values of voltage and current as follows:
$$P=V_{RMS} I_{RMS} \cos(\theta_v - \theta_i) (Eq. 12.16)$$
And:
$$Q = V_{RMS} I_{RMS} \sin(\theta_v - \theta_i) (Eq. 12.17)$$
Section Summary
- The RMS value of a sinusoidal signal $f(t) = F_m \cos(\omega t + \theta)$ is given by:
$$f_{RMS} = \frac{F_m}{\sqrt{2}}$$
- The above formula cannot be used for any signal other than a pure sinusoid with no offset.
Exercises
- The current and voltage delivered to a load are $i(t) = 2 \cos(100t)$ and $v(t) = 120 \cos(100t+65^{\circ})$, respectively. What are the RMS values of voltage and current?
12.4: Apparent Power and Power Factor
In the previous subsections, we have seen that average power can be represented in terms of either the magnitudes of the voltage and current or the RMS values of the voltage and current and a multiplicative factor consisting of the cosine of the difference between the voltage phase and the current phase:
$$P= \frac{V_m I_m}{2} \cos(\theta_v - \theta_i) = V_{RMS} I_{RMS} \cos(\theta_v - \theta_i)$$
It is sometimes convenient to think of the average power as being the product of apparent power and a power factor (abbreviated $pf$). These are defined below:
- The apparent power is defined as either $\frac{V_m I_m}{2}$ or $V_{RMS} I_{RMS}$. (The two terms are, of course, equivalent.) Units of apparent power are designated as volt-amperes (abbreviated VA) to differentiate apparent power from either average power or reactive power.
- The power factor is defined as $\cos(\theta_v - \theta_i)$. Since cosine is an even function (the sign of the function is independent of the sign of the argument), the power factor does not indicate whether the voltage is leading or lagging the current. Thus, power factor is said to be either leading (if current leads voltage) or lagging (if current lags voltage).
It should be emphasized again at this point that the voltage and current are not independent quantities; they are related by the load impedance. For the system of Figure 12.1, for example, the voltage and current phasors are:
$$\underline{V} = Z_L \cdot \underline{I} (Eq. 12.18)$$
Where $\underline{V}$ is the voltage phasor across the load, $\underline{I}$ is the current phasor through the load, and $Z_L$ is the load impedance. Thus, the difference between the voltage and current phase angles is simply the phase angle of the load impedance: $\theta_v - \theta_i = \angle \theta_{ZL}$. Therefore, the load impedance sets the power factor. If the load is purely resistive, $\theta_v = \theta_i$, the power factor is one, and the average power is the same as the apparent power. If the load is purely imaginary (as with purely inductive or purely capacitive loads) the power factor is zero and there is no average or real power absorbed by the load.
Section Summary
- Apparent power and power factor provide an alternate method for characterizing the average power delivered to the load. If the average power is:
$$P= \frac{V_m I_m}{2} \cos(\theta_v - \theta_i)$$
The apparent power is $\frac{V_m I_m}{2}$ and the power factor is $\cos(\theta_v - \theta_i)$.
Exercises
- The current and voltage delivered to a load are $i(t) = 2 \cos(100t)$ and $v(t) = 120 \cos(100t+65^{\circ})$, respectively. What are the apparent power and power factor of the power delivered to the load?
- A load consumes 100kW with a power factor $pf = 0.85$ (lagging). If the load current is 256A (RMS), find the load voltage.
- An industrial plant has a load which consumes 20kW of power from a $220V_{RMS}$ line. If the power factor is 0.9 (lagging), what is the difference in angle between the load voltage and the load current?
12.5: Complex Power
Apparent power, average power, reactive power, and power factor can all be represented simultaneously in a single parameter called complex power. If we define complex power as:
$$S= \frac{\underline{VI}^{*}}{2} (Eq. 12.19)$$
Where $\underline{V}$ is the phasor representing the voltage, $\underline{I}$ is the phasor representing the current, and the superscript * denotes complex conjugation (simply changing the sign on the imaginary part of the phasor).
If we substitute the magnitude and phase angle representations for the phasors in equation (12.19), we obtain (since complex conjugation simple changes the sign of the phase angle of a complex number):
$$S = \frac{1}{2} (V_m \angle \theta_v) (I_m \angle - \theta_i) = \frac{V_m I_m}{2} \angle (\theta_v - \theta_i) (Eq. 12.20)$$
So that the complex power $S$ is a complex number with magnitude $\frac{V_m I_m}{2}$ (or, equivalently, $V_{RMS} I_{RMS}$) and phase angle $\theta_v - \theta_i$. It is easy to see that the magnitude of the comples power is simply the apparent power.
If we represent $S$ in rectangular coordinates, we obtain:
$$S=P+jQ (Eq. 12.21)$$
Where $P$ is the average power:
$$P=\frac{V_m I_M}{2} \cos(\theta_v - \theta_i) = V_{RMS} I_{RMS} \cos(\theta_v - \theta_i)$$
As before, and Q is the reactive power:
$$Q= \frac{V_m I_m}{2} \sin(\theta_v - \theta_i) = V_{RMS} I_{RMS} \sin(\theta_v - \theta_i)$$
Also as before.
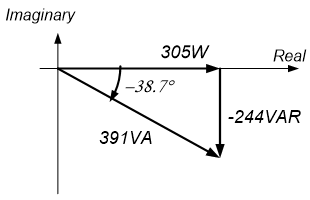
The complex power, real power, reactive power, and apparent power can be represented graphically in the complex plane as a power triangle, as shown in Figure 12.4 below.
One important thing to note about Figure 12.4 is that this figure differs from a phasor diagram – the components shown on the power triangle are not phasors, since they do not provide magnitude and phase information about sinusoidal signals. The vectors shown in Figure 12.4 are simply complex numbers.
We conclude this chapter with an example.
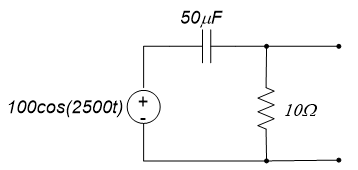
Example 12.1
For the circuit below,
- Find the average power delivered by the source
- Find the power absorbed by the resistor
- Find the apparent, real, and reactive powers delivered by the source
- Sketch a power triangle for the source
The frequency domain circuit is shown below.
The current delivered by the source is therefore:
$$\underline{I} = \frac{100 \angle 0^{\circ}}{(10-j8)\Omega} = 7.8 \angle 38.66^{\circ} A$$
- The average power delivered by the source is therefore:
$$P=\frac{(100V)(7.8A)}{2} \cos(0^{\circ} - 38.66^{\circ}) = 305W$$
- The power absorbed by the resistor is the same as the average power delivered by the source, so $P_{10\Omega}=305W$, which is the same as $R \cdot I^2_{RMS}$.
- The apparent power is $\frac{(100V)(7.8A)}{2}=391VA$, the reactive power is $Q = \frac{(100V)(7.8A)}{2} \sin(0^{\circ}-38.66^{\circ}) = -244VAR$, and the real power is simply the average power, $P=305W$.
- The power triangle is shown below:
Section Summary
- It is often convenient to express power as a complex number, S. This quantity expresses, simultaneously, the average power, the reactive power, the apparent power, and the power factor. Complex power can be determined from the voltage and current phasors as:
$$S=\frac{\underline{VI}^{*}}{2}$$
Where * denotes complex conjugation.
- As with any other complex number, complex power can be expressed in either rectangular or polar coordinates.
- In rectangular coordinates, the complex power readily provides the real power ($P$) and reactive power ($Q$):
$$S=P+jQ$$
- In polar coordinates, the complex power readily provides the apparent power and power factor:
$$S=\frac{V_m I_m}{2} \angle (\theta_v - \theta_i)$$
Where the apparent power is $\frac{V_m I_m}{2}$ and the power factor is given by $\cos(\theta_v - \theta_i)$.
Exercises
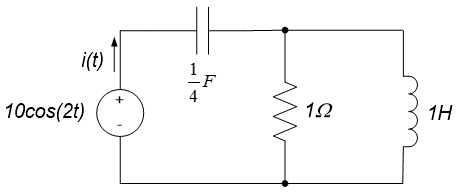
1. The current and voltage delivered to a load are $i(t) = 2 \cos(100t-30${\circ})$ and $v(t) = 120 \cos(100t+65^{\circ})$, respectively. What is the complex power delivered to the load?
2. For the circuit shown, $i(t) = 2 \cos(100t)$ and $v(t) = 120 \cos(100t+65^{\circ})$. Find:
- The complex power delivered by the source
- The average power delivered by the source
- The power dissipated by the resistor
3. For the circuit shown, find
- $i(t)$
- The complex power delivered by the source
- The average power delivered by the source
12.6: Power Factor Correction
In previous sections, we saw that power can be considered to be real (average power) or imaginary (reactive power). Reactive power is power which is provided to energy storage elements such as inductors or capacitors; this power is returned to the power source, since inductors and capacitors have no energy dissipation mechanism. The power factor provides a metric for assessing the amount of real power relative to the reactive power delivered to a load. The higher the power factor, the larger the amount of real power relative to reactive power – ideally, a power factor of one means that no reactive power is provided to the load.
Power companies in general cannot charge customers for power which is returned to the power company, so delivering reactive power to a customer is not productive from a power company’s standpoint. In fact, since transmission losses will typically result in real power losses due to transmission of reactive power, the power company actually loses power when transmitting reactive power, for which no one pays! Unsurprisingly, this is not popular with power companies.
Large power users, such as factories, may have requirements placed upon them by the power company to provide a minimum power factor for their loads. If the factory cannot meet the required power factor, the power company can refuse to supply power or charge an increased rate for the power they do provide. This chapter illustrates how to re-design an inductive load to increase its power factor.
Most large power users’ loads are inductive in nature. Therefore, in this section, we will only consider power factor correction for inductive loads. We illustrate the overall process in the context of an example.
Example 12.2
Determine the power factor for the circuit below if $vs(t)=100 \cos(377t)$. Re-design the load so that the power factor is one.
The load in this case consists of a $100\Omega$ resistor in parallel with a 1H inductor. To determine the power factor, we need to determine the current delivered by the source; we do this by determining the equivalent impedance of the load, $Z_L$:
$$Z_L = \frac{(100 \Omega)(j377 \Omega)}{100 \Omega + j377 \Omega} = 96.67 \angle 14.86^{\circ}$$
Therefore, the current phasor delivered by the source is:
$$\underline{I}_s = \frac{\underline{V}_s}{Z_L} = \frac{100 \angle 0^{\circ}}{96.67 \angle 14.86^{\circ}} = 1.03 \angle - 14.86^{\circ}$$
The power factor is:
$$pf = \cos(\theta_v - \theta_i) = \cos(0^{\circ} - (-14,86^{\circ})) = 0.967 \text{(lagging)}$$
Note that the power factor is lagging, since current lags voltage, this is because the load is inductive in nature.
We can change the power factor of the load by adding a capacitor in parallel with the inductive load. The impedance of the capacitor can be used, in essence, to cancel out the inductive impedance of the load. The re- designed circuit is as shown below. The capacitance, C, must be chosen to provide the desired power factor.
In order to determine the necessary size of the capacitor, we first determine the reactive power of the uncompensated system. Without the capacitor, the reactive power is:
$$Q= \frac{V_m I_m}{2} \sin(\theta_v - \theta_i) = \frac{(100V)(1.03A)}{2} \sin(14.86^{\circ}) = 13.26 VAR$$
Our goal is to use the capacitor to change this reactive power so that the resulting power factor is as desired, without changing the real power delivered to the load. The capacitor will induce a negative reactive power; in order to achieve a power factor of exactly one, the reactive power introduced by the capacitor must exactly cancel the reactive power of the original load. Thus, the capacitor’s reactive power must be:
$$Q_C = -13.26 VAR$$
For the parallel combination of the resistor, capacitor, and inductor, we can claim:
$$|Q_C| = \frac{V^2_{RMS}}{|Z_C|} = \frac{V^2_{RMS}}{|\frac{1}{\omega C}|} = \omega CV^2_{RMS}$$
Where $|Q_C|$ is the magnitude of the desired reactive power, and $|Z_C|$ is the magnitude of the capactior's impedance. Solving the above expression for the desired capacitance provides:
$$C = \frac{|Q_C|}{\omega V^2_{RMS}} = \frac{13.26VAR}{(377 \text{rad/sec}) (\frac{100}{\sqrt{2}^V})} = 4 \mu F$$
And a $7 \mu F$ capacitor placed in parallel with the load will give the desired $pf = 1$.
Section Summary
- A small power factor means that a large portion of the power delivered by the power company to a user is in the form of reactive power. The user does not pay for reactive power, since it is essentially returned to the power company. The power company, however, incurs costs in exchanging reactive power with the user, since transmission of the reactive power results in power dissipation. Power companies, therefore, may require that a user meet a minimum power factor requirement.
- The power factor of an inductive load can be increased by placing a capacitor in parallel with the load. This process is called power factor correction. The goal is to increase the power factor without changing the average power delivered to the load.